Dijkstra

image-20201114225526432

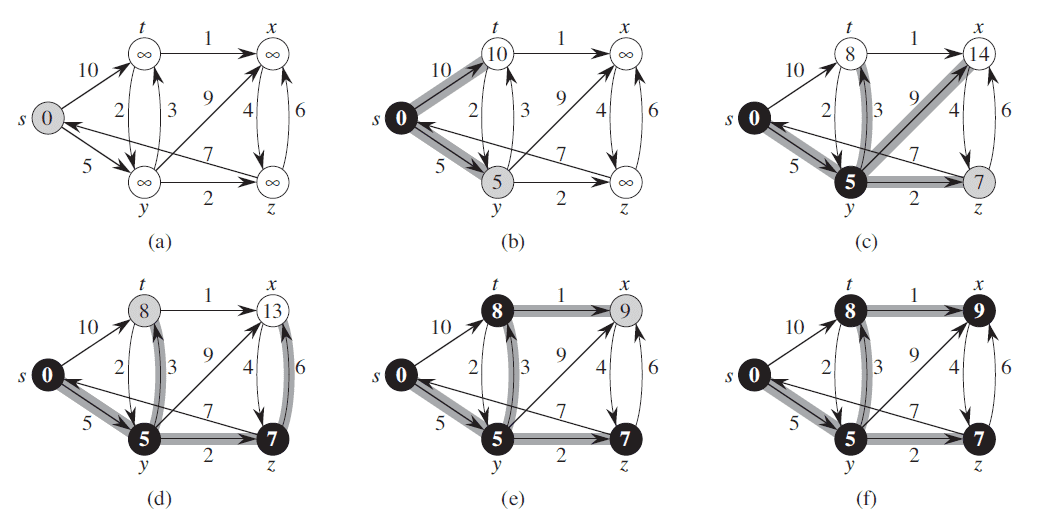
(图片来源 : CLRS p659 24.3)

原版算法

先来看看代码

import math, heapq

for u in vertex:  # 这边对所有点都进行了一次 Dijkstra
    heap = []
    for v in vertex:
        if v != u:
            heapq.heappush(heap, [adj[u][v] if v in adj[u] else math.inf, v])  #提取到达距离最小的节点
    dist = {u: 0}
    while len(heap) > 0:
        mindist, v = heapq.heappop(heap)
        dist[v] = mindist
        for i in range(len(heap)):
            if heap[i][1] in adj[v]:
                heap[i][0] = min(heap[i][0], mindist + adj[v][heap[i][1]])
        heapq.heapify(heap)
        

伪代码：

Dijkstra(G,w,s): 初始化，标记所有点距离为正无穷 S = $\varnothing$ Q = V- S while Q $\ne \varnothing:$ u = Extract-Min(Q) S = S $\cup$ {u} 对所有 u 的邻接点 v: Relax(u,v,w)

def Relax(u,v,w):
	if d[v] > d[u] + w:
        d[v] = d[u] + w

正确性分析

辅助定理 1: $d[v] \ge \delta(s,v),\ \delta(s,v)$ 为 s 到 v 的最短路径

无论怎么 relax，对于所有目的地终点，我们都不可能得到一个比最短路径还小的答案，可以用数学归纳法证明：

初始化阶段，$d[s]=0,d[v]= \inf$ ，成立

假设： 直到第 j 次 relax，定理仍然成立，则 $d[j] \ge \delta(s,j)$。

假设： 第一次违背定理出现在第 i 次 relax，使得 $d[i]<\delta(s,i)$, 那么在第 i 次 relax 时候：

$$d[i] = d[j] + w(j,i) < \delta(s,i)\\ while\ d[j] + w(j,i) \ge \delta(s,j) + w(j,i)\\ \ge \delta(s,j) + \delta(j,i)\\ \ge \delta(s,i)$$

得证。

定理 2: 当 Dijkstra 结束的时候，所有点都满足：$d[v] = \delta(s,v)$

要证明以上定理，可以先证明当 v 被加进到 S 集合后，$d[v] = \delta(s,v)$ ， 且 d[v] 不会改变。

同样我们利用反正法：

假设： 当 u 被加入到 S 中后，定理 2 第一次被违背。

当 u 将要被加入到 S 中时，$d[u] \ne \delta(s,u) \because theory 1 \therefore d[u] > \delta(s,u)$

见下图， 假设 P 为 S 到 u 的最短路径， 从起始点 s 出发沿 P 行走， $X \rightarrow Y$ 是第一条走出 S 集合的路径，及 P 路径上 x 前的所有点都在 S 集合内，y 之后的所有点都在 S 集合外。

所以在定理 2 第一次被违背前，最后一个被加入到 S 集合的点为 x, $d[x] = \delta(s,x)$ （因为我们假设第一次违背定理 2 在 u）。

X 被加入 S 后我们对 x 的所有邻接点 relax， 包括 y。

1. 如果在 relax 前 $d[y] = \delta(s,y)$， 那么 relax 后 $d[y] = \delta(s,y)$ .
2. 如果在 relax 前$d[y] > \delta(s,y)$, 那么 relax 后 $d[y] = d[x] + w(x,y) = \delta(s,y)$

所以 relax 后，$d[y] = \delta(s,y)$ 一直成立。

我们有 $d[y] = \delta(s,y) < \delta(s,u)$，但我们没有选择加入 y 到 S 而是加入了 u，说明 $d[u] < d[y] < \delta(s,u)$，违反了 辅助定理 1 .

得证。

image-20201115113459433

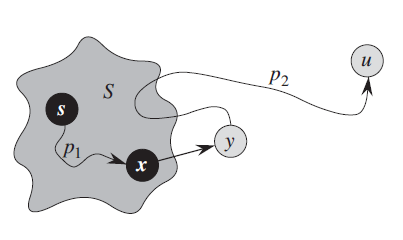
​ （图片来源：CLRS：p660）

时间复杂度

for u in vertex:  ## 对所有点都进行了一次 Dijkstra
    heap = [] 
    for v in vertex:  # 建一个 heap O(V)
        if v != u:
            heapq.heappush(heap, [adj[u][v] if v in adj[u] else math.inf, v])  
    dist = {u: 0}
    while len(heap) > 0:  # V 次
        mindist, v = heapq.heappop(heap) # O(lgV)
        dist[v] = mindist
        for i in range(len(heap)): # 总的讲，我们要做 E 次 relax
            if heap[i][1] in adj[v]:  # 每次判断最坏用 V  
                heap[i][0] = min(heap[i][0], mindist + adj[v][heap[i][1]])  
                # O（1）如果 relax 完之后不马上进行 heapify
                # O（lgV）如果 relax 完之后马上进行 heapify
        heapq.heapify(heap)    #这里的 heapify 是对整个 heap 进行重新排序，不是对一个点。你也可以选择在 relax 之后马上对相应的点进行 heapify，总消耗 O(Elgv)

所以上面这种方法，时间复杂度为：$O(V lgV + E lgV + EV)$ ，当然我们可以对他进行优化，在用字典的方式记录每个 v 在 heap 中的位置以节省 relax 前搜索字典位置的时间，用 Fibonacci Heap 来优化每次 relax 中修改 heap 值的时间，最终时间复杂度可以提高为： $O(V lgV + E)$

特殊想法

考虑以下的这些特点，我给出几个应用 Dijkstra 的要点如下：

• 虽说 Dijkstra 为单点对端路径优化(single source)的方案，他计算了一个点到其他所有点的最短路径。然而当你的最终目的地有多个可选项时可以却可以采用 Dijkstra，只需要反向计算，从目的地出发计算每个城市到目的地的最短路径。本案例中讲所有的最终目的地点当成一个整体来计算，使得这个问题从一个多点出发最短路径问题，变成了单点出发最短路径问题。

  总结关键词： 反向计算路径 ， 节点合并

• Dijkstra 虽然快，但是局限性也大，排序要求使得他不能够再分布式系统中计算，所以相对的应用没有其他一些最短路径算法那么多，如 Bellman

以下的情景概述也许可以帮助理解：

新冠来袭而你依旧深处国外，担心安危的你下定决心要用最短的时间回到中国。然而当你打开某机票网站却发现一张直达机票都没有了，现在唯一可行的方案就是从别的地方转机：

• 很悲剧的告诉你你可能要转好几次机。

• 健康码分为绿，橙，红三种，有些航空公司要求你拿到 当地政府 的绿码才能够登机，有些只会要求你橙了就可以登机， 但是你不能拿着前一个城市给的健康码去另一个城市登机。

• 当你拿着绿码抵达某个转机城市，该城市可能给你绿码，也可能会给你提升危险登记变为橙码。这取决于对乘客来源地的信任。同理橙码能够变成红码。

• 可以通过隔离来提升自己的安全等级，每个城市有不同的隔离政策，对提升健康码等级的隔离天数也有不同要求。

你手中拥有如下数据：

• qrtn: 每个城市升级健康码所需的隔离天数：[红到橙，橙到绿]
• roadmap_raw: 城市航班信息："城市 id1:城市 id2:所需天数 城市 3:城市 4:所需天数"
• target_city_list: 你要的目的地的代码

详细请参考下面这个例子：

• 例子中 qrtn 包含 7 个元素，第一个 0 占位用请忽略。第 1 个元素及 qrtn[1] 表示在城市 1，讲橙码升级到绿码要 7 天，讲红码升级到橙码要 14 天。
• 例子中 roadmap_raw 包含 6 个城市信息，用空格分开。1:2:10 表示 id 为 1 的城市到 id 为 2 的城市需要 10 天。其中所需天数 10 为正表示两个城市之间互相信任，为负表示城市不信任，你的安全码要被降一级。
• 例子中 target_city_list 说明你最终要到达 id 为 3 或 id 为 1 的城市。
• 在这里我们假设所有城市都要求需要橙码才能登机。

qrtn = [0，[14,7],[14,7],[21,7],[13,10],[21,2],[7,14]]
roadmap_raw = "1:2:10 1:4:-15 2:4:10 2:5:45 3:4:-10 3:6:20"
target_city_list = [3,1]