Elliptic Curve Cryptography | 椭圆曲线加密概念

Kevin 吴嘉文大约 9 分钟

椭圆曲线加密

公钥密码体制在一定程度上解决了对称密码体制存在的密钥分发管理，可否认性等问题。常见的公钥密码体制由 RSA， ElGamal 和椭圆曲线公钥密码。本文对 ECC 椭圆曲线公钥密码进行理论梳理与简要的介绍，要落实到实际的应用中还需对方案本身升级打补丁。

群

定义：设 G 是一个非空集合，并在 $G$ 内定义了一种代数运算 “ $\circ$ ”，若满足：

封闭性。对任意 $a, b \in G,$ 恒有 $a \circ b \in G$
结合律。对任意 $a, b, c \in G,$ 恒有 $(a \circ b) \circ c=a \circ(b \circ c)$
$G$ 中存在一恒等元 e，对任意 $a \in G,$ 使 $a \circ e=e \circ a=a$
对任意 $a \in G,$ 存在 $a$ 的逆元 $a^{-1} \in G,$ 使 $a \circ a^{-1}=a^{-1} \circ a=e$ 则称 $G$ 构成一个群。
若加法，恒等元用 0 表示，
若为乘法，恒等元称为单位元

性质

群的恒等元、每个元素的逆元都是唯一的
若 $a,b \in G, \therefore (a*b)^{-1} = b^{-1}*a^{-1}$
唯一解： $\forall a,b \in G, a*x = b$ 和 $y*a = b$ 在 G 中有唯一解 $x = a^{-1} *b,y = b*a^{-1}$
消除律： $a * x = a * y$ 可得 $x = y$

环

定义：非空集合 $R$ 中存在加和乘运算，且满足:

$R$ 在加法运算下构成阿贝尔群
乘法有封闭性
乘法结合律成立，且加和乘之间有分配律

域

定义：非空集合 F，若 F 中定义了加与乘两种运算，且满足:

F 关于加法构成阿贝尔群，加法恒等元记为 0
F 中所有非零元素对乘法构成阿贝尔群，乘法恒等元为 1
加法与乘法之间满足分配律

元素个数无限的域为无限域，元素个数有限的域为有限域（或伽逻华域）， $GF(q)$ 或 $F_q$ 表示 $q$ 阶有限域， 有限域的元素个数为有限域的阶 。素域：设 $p$ 为素数，则整数全体关于模 $p$ 的剩余类在 模 p 的运算 下（模 $p$ 加和乘）构成 p 阶域 $GF(p)$ .

域的运算法则： 域的基础运算为加法与乘法。域元素的减法由加法定义，即 $a-b = a + (-b)$ ， $-b$ 是 $b$ 的负元，是使得 $b+-b = 0$ 的唯一一个域元素。除法（逆运算）由乘法定义，即 $a/b = a * b^{-1}$ ，其中 $b^{-1}$ 是 b 的逆元，是使得 $b*b^{-1} = 1$ 成立的唯一一个域元素。

阿贝尔群

定义：

如果群 $<G,*>$ 中的运算是可交换的，则称该群为阿贝尔群，或称交换群 定理：
设 $<G,*>$ 是一个群， $<G,*>$ 是阿贝尔群的充要条件是对任意的 a，b∈G，有 $(a*b)*(a*b)=(a*a)*(b*b)$ 。
任何一个循环群必定是阿贝尔群。

阿贝尔群中的交换律与结合律是双方用户在椭圆曲线公钥体制能够协商出相同密钥的基础。

椭圆曲线

本节包含的所有代码均为演示代码，该代码仅为理解提供加法运算帮助。实际使用 ECC，需要在域运算上是实现时间与空间复杂度更多的优化

椭圆曲线为以下方程： $y^2 + axy + by = x^3 + cx^2 + dx + e$

该方程也成为 $Weiersrass$ 方程，使用变量的相容性简化，可得到：

对于素域有： $y^2 = x^3 + ax + b$ ， $(a,b \in GF(p), \Delta = -16 (4a^3 + 27b^2) \ne 0 )$ 对于二进制域有： $y^2 + xy = x^3 + ax + b$ 本文只讨论素域

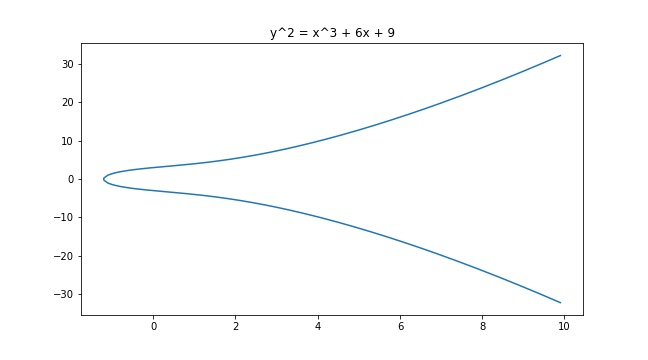
图：有些椭圆曲线长这样

椭圆曲线性质

$\Delta= -16(4a^3+27b) \neq 0$ ，保证曲线性状光滑，连续，所有的点没有两个或两个以上不同的切线
$a,b \in K, K$ 为 $E$ 的基础域
点 $O_{inf}$ 是曲线的唯一的无穷远点。

运算法则

恒等元（单位元） 为无穷远点 $O_{\inf}$ 为恒等元， $P + O_{\inf} = P$ 逆元（负元素） 为该点关于 X 轴的对称点。 点加运算： 椭圆曲线上 $P = (x_1,y_1),Q = (x_2,y_2)$ 两点相加：做两点直线 $PQ$ （如果 $P=Q$ ，那么就做切线），相交椭圆曲线于第三点 $-R,-R$ 的逆元 $R = (x_3,y_3)$ 即为运算结果。记为： $P+Q = R$ ，

x_{3}=\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)^{2}-x_{1}-x_{2}\\ \text { } y_{3}=\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\left(x_{1}-x_{3}\right)-y_{1}

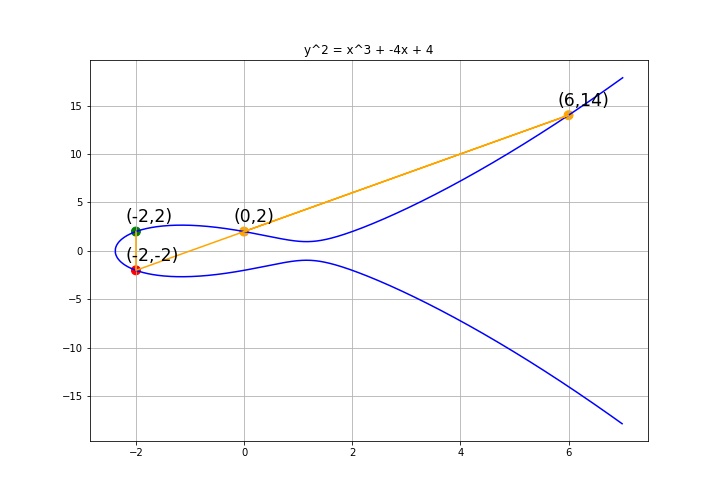
图：点加运算示例

如上图，在曲线 $y^2 = x^3 -4x + 4$ 中， $P = (0,2), Q = (6,14)$ ， $PQ$ 交椭圆曲线于点 $-R = (-2,-2),-R$ 的逆元为 $R = (-2,2)$ 。所以 $P + Q = R$

乘法运算： 令 $P = (x_1,y_1), P \ne -P$ 则 $3P = P + P + P$ ，就是通过上述的加法法则执行 3 次。

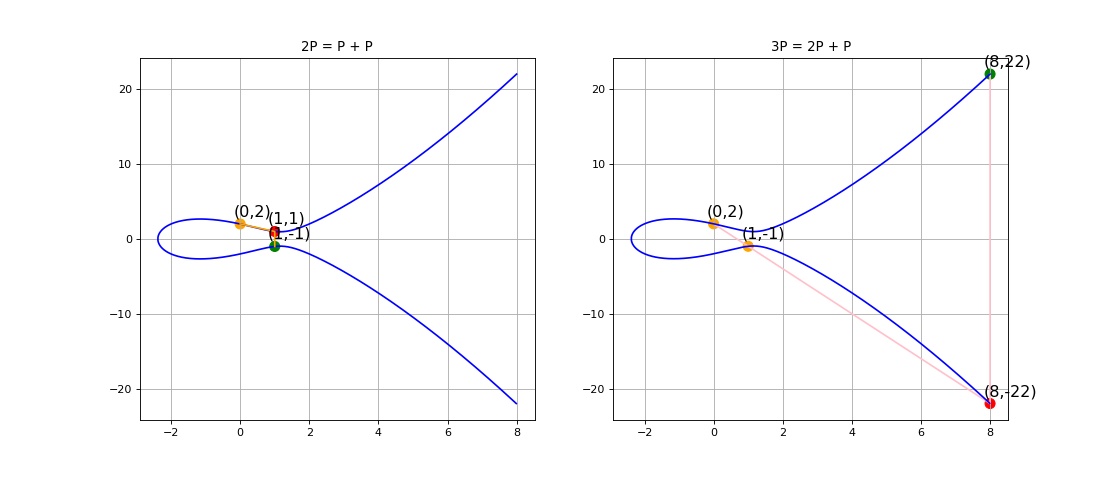
图：倍点运算 3P = P+P+P

有限素域的椭圆曲线

给定 p 阶有限域 $GF(p)$ ， $p$ 为素数，椭圆曲线上的点集 $E_p(a,b)$ 中的点 (x，y) 满足 $y^2 = x^3 + ax + b \mod p$ ， $0 \le x,y\le p, x,y \in Z$

点集：如给定 $p = 13$ ，已经椭圆曲线方程 $y^2 = x^3 -4x + 4 \mod 13$ ，点集 $E_{13}(-4,4)$ 中的点有 $(0, 2), (0, 11), (1, 1), (1, 12), (2, 2), (2, 11), (4, 0), (6, 1), (6, 12), (8, 4), (8, 9), (11, 2), (11, 11),O_{inf}$

a，b，p = -4，4，13
E_p = [(x，y) for x in range(p) for y in range(p) if  y **2 %p  == (x** 3 + a*x + b)%p  ]
print(f"给定 p= {p}，a = {a}，b = {b}， Ep 点集上的点有：\n"，E_p)

给定 p= 13，a = -4，b = 4， Ep 点集上的点有：
 [(0， 2)， (0， 11)， (1， 1)， (1， 12)， (2， 2)， (2， 11)， (4， 0)， (6， 1)， (6， 12)， (8， 4)， (8， 9)， (11， 2)， (11， 11)] 以及 无穷远点

有限域运算 当 $4a^3+27b^2 \ne 0 (mod\ p)$ 以下运算成立：

设 $P(x_1,y_1), Q(x_2,y_2) \in E_{p}(a, b),$ $P$ 的逆元为 $(x,-y \mod p) = (x,p-y)$ ，设 $P \neq-Q,$ 则 $P+Q=\left(x_{3}, y_{3}\right)$

\begin{array}{l} x_{3} \equiv \lambda^{2}-x_{1}-x_{2}(\bmod p) \\ y_{3} \equiv \lambda\left(x_{1}-x_{3}\right)-y_{1}(\bmod p) \end{array}

其中

\lambda=\left\{\begin{array}{l} \frac{y_{2}-y_{1}}{x_{2}-x_{1}},if\ P \neq Q \\ \frac{3 x_{1}^{2}+a}{2 y_{1}}, if\ P=Q\ and\ P \ne -P \end{array}\right.

例：下图中 $P = (0,11) , Q = ( 4,0)$ ，带入上述公式得出 $P+Q = R = (6,12)$ 。 对于不熟悉域的朋友：域运算中的除法（逆运算）于欧式四则运算除法不同。如 $1 \div 2 \mod 7 = 4$ 而不是 $\frac 1 2$ ，应先对 2 求逆元然后再乘 1

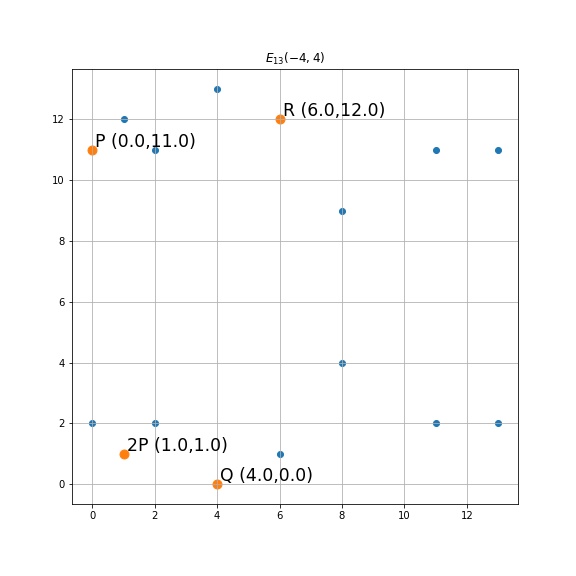
图：有限域运算

相关代码

#  **域的点加运算** 
def addition(P,Q,a,b,p):
    (x1,y1),(x2,y2) = P,Q
    L =(y2 - y1)* devision((x2 - x1),p) if P != Q else(3*x1**2+a)* devision((2*y1),p)
    x3 = (L**2 - x1 - x2)%p
    y3 = (L*(x1 - x3) - y1 )%p
    return x3,y3

#  **基于 Euclidean 算法的域除法(逆运算)**  
def devision(a,p):
    """
    return a**-1 mod p\
    
    """
    a %= p
    d,x,y,x1 = Euclidean(a,p)
    return x % p
    
    
def Euclidean(a，b):
    """
    输入整数 int a， int b;
    返回 int d = gcd(a，b); (int x，int y)，where ax + by = d
    """
    u,v = a,b
    x1,y1,x2,y2 = 1,0,0,1
    while u != 0:
        q = int(v/u)
        r = v - q*u
        x = x2 - q*x1
        y = y2 - q*y1
        v,u,x2,x1,y2,y1 = u,r,x1,x,y1,y
    d,x,y = v,x2,y2
    return d,x,y,x1

因 $Euclidean(a,p)$ 的输出结果 $d,x,y$ 满足： $a*x + p*y = d \because p is prime, \therefore d = 1$ ，根据逆元的定义 $a * a^{-1} = 1 \mod p$ ， $\because a*x \mod p = 1,\ x\mod p= a^{-1}$ 。因此可以用 $Euclidean$ 求出整数 $a$ 的逆元。

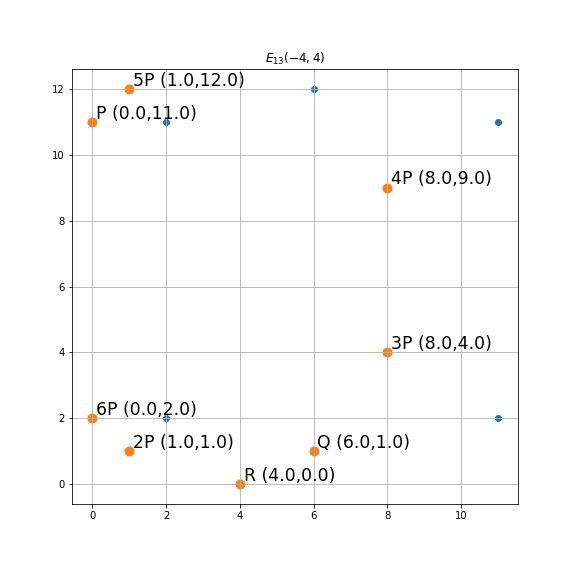
域中点的阶 给定一椭圆曲线， $P$ 为曲线上一点，存在最小正整数 $n$ 使得 $nP = O_{inf}$ ，等价于 $(n-1)P = -P$ ，则 $n$ 为该曲线的阶。若 $n$ 不存在，则曲线是无阶的。

下图例中，点集为 $E_{13}(-4,4),P = (0,11)$ 。 $P$ 的阶为 7， $6P = (0,2)$

NIST 素数 部分特殊的素数模能够使 ECC 的运算具有更高的效率，如

p_{192} = 2^{192}-2^{64} - 1\\ p_{224} = 2^{224}-2^{96} + 1\\ p_{256} = 2^{256}-2^{224} + 2^{192} + 2^{96} - 1\\ p_{384} = 2^{384} - 2^{128}-2^{96} + 2^{32} - 1\\ p_{521} = 2^{521}- 1\\

一部分原因是这些模都可以表示成少量的 2 的幂的表达式。并且幂都是 32 的倍数，这在 32 位的计算机有运行优势

投影坐标 点加与倍点需要使用到大量的域乘法与除法（逆）运算。使用投影坐标来表示域中的点可以解决域除法（逆）运算比乘法费时的问题。

椭圆曲线离散对数问题 ECDLP

给定定义与有限域 $F _q$ 上的椭圆曲线 $E$ ，基点 $G\in E(F_q)$ ，阶为 $n$ ，点 $Q \in\ <P>$ ，寻找一个整数 $L$ 使得 $Q = LP$ 。整数 $L$ 为 $Q$ 的基于 $P$ 的离散对数，表示为 $L = log_p(Q)$ 。目前攻击 ECDLP 最有效的 Pohlig-Hellman 和 Pollard's rho 算法时间复杂度为 $O(\sqrt p)$ 。

椭圆曲线离散对数问题现在并没有被证明为 NP-hard，之所以大家都在用，可能是因为到目前为止仍没有人发现一种有效的破解方法。然而没人知道 ECDLP 是否存在一种有效的破解的方法。

椭圆曲线 Diffie-Hellman 问题 ECDH

在加密前，Bob 和 Alice 共享以下信息，同时假设该加密算法公开，即大众可以也知道这些共享信息：

椭圆曲线 $y^2 = x^3 + ax + b$
共享素数 $p$ ，即域的阶
基点 $G$
基点的阶 $n$
余因子 $h = \#E(F_q)/n$
由以上信息可得点集 $Ep(a,b)$

ECDH 流程简介

假设密钥交换双方为 Alice、Bob，其有共享曲线参数:

椭圆曲线 $y^2 = x^3 -4x + 4$
共享素数 $13$ ，即域的阶
基点 $(1,1)$
基点的阶 $7$
余因子 $h = \#E(F_q)/n$

Alice 生成随机整数 $a = 3$ , 生成的随机整数即为 Alice 的私钥，并且私钥不能够大于基点的阶，计算 $A=3G=(0,2)$ 。
Bob 生成随机整数 $b=4$ ，计算 $B=4G = (0,11)$ , 即生产 Bob 公钥
Alice 将 $A$ 传递给 Bob。传递可以公开。
Bob 将 $B$ 传递给 Alice。
Bob 收到 Alice 传递的 A，计算共同秘密 $Q =b*A = 4*(0,2) = (8,4)$
Alice 收到 Bob 传递的 B，计算 $Q=a*B = 3*(0,11) = (8,4)$

Alice、Bob 双方即得 $Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q'$ 即双方得到一致的密钥 $Q$ 。

安全性约束：

抵御 ECDLP 中 Pohlig-Hellman 攻击， $\#E(F_q) = nh$ 应满足 n 为素数且大于 $2^{160}$ ，h 非常小。

抵御同构攻击，Weil 和 Tate 配对攻击，应满足 $\#E(F_q) \ne q$ , $\forall 1\le k \le C, C$ 足够大, $n$ 不被 $q^k - 1$ 整除。

Elliptic Curve Cryptography | 椭圆曲线加密概念

# 椭圆曲线加密

# 群

# 环

# 域

# 阿贝尔群

# 椭圆曲线

# 运算法则

# 有限素域的椭圆曲线

# 椭圆曲线离散对数问题 ECDLP

# 椭圆曲线 Diffie-Hellman 问题 ECDH

# ECDH 流程简介