白板机械学习笔书|线性回归

线性回归基础数学。笔记思路源于 shuhuai-白板机械学习 系列教程。

线性回归基础

最小二乘法

最小二乘法矩阵表达的损失函数：

$$L(W)=\sum_{i=1}^{N}\left\|W^{T} x_{i}-y_{i}\right\|^{2}$$

我们的目标就是使得以上的均方差最小。对齐求导并令导数为零。

$$\frac{\partial L(W)}{\partial W}=2 X^{T} X W-2 X^{T} Y=0\\ W = (X^TX)^{-1}X^TY$$

几何意义

将 $X_{N\times p}$ 中的每一列看做一个向量，那么 $X$ 可以看做一个 $p$ 维空间。

image-20220314153519256

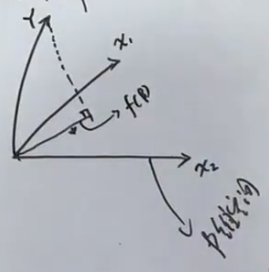
$Y$ 不在该空间内，因此 $Y$ 在该平面内的投影就是误差最小的预测值。假设 $Y$ 的投影在 $X_{N\times p}W_{p\times 1}$ 上，那么虚线为 $Y-XW$。

虚线垂直与 $X$，所以 $X^T(Y-WX)=0$。求得 $W = (X^TX)^{-1}X^TY$

从概率角度看，最小二乘法即为假设噪声符合高斯分布的最大似然估计。

假设 $y \mid X, W \sim N\left(W^{T} X, \sigma^{2}\right)$

使用最大似然估计求解：

$$\begin{aligned} L(W) &=\log p(y \mid X, W) \\ &=\log \prod_{i=1}^{N} p\left(y_{i} \mid x_{i}, W\right) \\ &=\sum_{i=1}^{N} \log p\left(y_{i} \mid x_{i}, W\right) \\ &=\sum_{i=1}^{N} \log \left(\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-W^{T} x_{i}\right)^{2}}{2 \sigma^{2}}\right)\right) \\ &=\sum_{i=1}^{N} \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{\left(y_{i}-W^{T} x_{i}\right)^{2}}{2 \sigma^{2}} \end{aligned}$$

$$\begin{array}{l} \hat{W}=\underset{W}{\operatorname{argmax}} L(W)\\ =\underset{W}{\operatorname{argmax}} \sum_{i=1}^{N} \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{\left(y_{i}-W^{T} x_{i}\right)^{2}}{2 \sigma^{2}}\\ =\underset{W}{\operatorname{argmax}} \sum_{i=1}^{N}-\frac{\left(y_{i}-W^{T} x_{i}\right)^{2}}{2 \sigma^{2}}\\ =\underset{W}{\operatorname{argmin}} \sum_{i=1}^{N} \frac{\left(y_{i}-W^{T} x_{i}\right)^{2}}{2 \sigma^{2}}\\ =\underset{W}{\operatorname{argmin}} \sum_{i=1}^{N}\left(y_{i}-W^{T} x_{i}\right)^{2} \end{array}$$

因此结果与上节最小化损失函数结果一样。 可以看出最小二乘估计假设了噪声服从正态分布。

正则化

从数学角度看 ，用上文方式求解最优 $W = (X^TX)^{-1}X^TY$ 时，若 $N \gg p$ 不成立，则 $X^TX$ 可能是不可逆的。导致不能求得 $W$ 的解析解。

添加了正则化后的损失函数为：

$$\begin{aligned} J(W) &=\sum_{i=1}^{N}\left\|W^{T} x_{i}-y_{i}\right\|^{2}+\lambda W^{T} W \\ &=\left(W^{T} X^{T}-Y^{T}\right)(X W-Y)+\lambda W^{T} W \\ &=W^{T} X^{T} X W-Y^{T} X W-W^{T} X^{T} Y+\lambda W^{T} W \\ &=W^{T} X^{T} X W-2 W^{T} X^{T} Y+\lambda W^{T} W \\ &=W^{T}\left(X^{T} X+\lambda I\right) W-2 W^{T} X^{T} Y \end{aligned}$$

令导数为零：

$$\frac{\partial J(W)}{\partial W}=2\left(X^{T} X+\lambda I\right) W-2 X^{T} Y=0\\ \hat{W}=\left(X^{T} X+\lambda I\right)^{-1} X^{T} Y$$

其中 $X^TX$ 为半正定，加上 $\lambda I$ 后为正定，即可逆。

从直观角度看，正则化系数越大，偏差也就越大，但也防止了过拟合。

加入了 L2 正则化的最小二乘估计其实也等价于服从高斯分布的噪声和先验的最大后验估计 MAP。 MAP 假设参数服从某个分布，而后根据先验知识对参数进行不断调整。数据越多，先验知识的主导地位越大。

给定：$y \mid X ; W \sim N\left(W^{T} X, \sigma^{2}\right)$ 假设 $W \sim N\left(0, \sigma_{0}^{2}\right)$

因此：

$$\begin{aligned} \hat{W} &=\underset{W}{\operatorname{argmax}} \operatorname{p(W|y)}\\ &=\underset{W}{\operatorname{argmax}} \frac{p(y \mid W) p(W)}{p(y)} \\ &=\underset{W}{\operatorname{argmax}} \operatorname{p(y|W)p(W)} \\ &=\underset{W}{\operatorname{argmax}} \log \{p(y \mid W) p(W)\} \\ &=\underset{W}{\operatorname{argmax}} \log \left\{\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{\left(y-W^{T} X\right)^{2}}{2 \sigma^{2}}\right\} \frac{1}{\sqrt{2 \pi} \sigma_{0}} \exp \left\{-\frac{\|W\|^{2}}{2 \sigma_{0}^{2}}\right\}\right\} \\ &=\underset{W}{\operatorname{argmax}}\log \left(\frac{1}{\sqrt{2 \pi} \sigma} \frac{1}{\sqrt{2 \pi} \sigma_{0}}\right)-\frac{\left(y-W^{T} X\right)^{2}}{2 \sigma^{2}}-\frac{\|W\|^{2}}{2 \sigma_{0}^{2}} \\ &=\underset{W}{\operatorname{argmax}}-\frac{\left(y-W^{T} X\right)^{2}}{2 \sigma^{2}}-\frac{\|W\|^{2}}{2 \sigma_{0}^{2}} \\ &=\underset{W}{\operatorname{argmin}} \frac{\left(y-W^{T} X\right)^{2}}{2 \sigma^{2}}+\frac{\|W\|^{2}}{2 \sigma_{0}^{2}} \\ &=\underset{W}{\operatorname{argmin}}\left(y-W^{T} X\right)^{2}+\frac{\sigma^{2}}{\sigma_{0}^{2}}\|W\|^{2} \\ &=\underset{W}{\operatorname{argmin}} \sum_{i=1}^{N}\left(y_{i}-W^{T} x_{i}\right)^{2}+\frac{\sigma^{2}}{\sigma_{0}^{2}}\|W\|^{2} \end{aligned}$$

这个结果与上一节中加入了 L2 正则化的损失函数一致。

线性分类

线性回归(Linear Regression)在统计机器学习中占据核心地位，其有三大特性： 线性 、 全局性 和 数据未加工性

非线性可能出现在三方面： 属性非线性，如多项式回归。 全局非线性，如激活函数非线性； 系数非线性，指系数不确定性，如神经网络（感知机）。

全局性指模型在全部特征空间上是恒定的，没有将特征空间划分为不同区域。决策树就不符合全局性。

数据未加工，即使用原始数据。如 PCA、流形都属于数据加工。

线性分类主要通过激活函数和降维带来分类效果

感知机

模型：

$$f(x)=\operatorname{sign}\left(w^{T} x\right) \quad x \in \mathbb{R}^{p}, w \in \mathbb{R}^{p}$$

其中 $sign$ 为正负符号

损失函数为预测错误的样本个数：

$$L(w)=\sum_{i=1}^{N} I\left\{y_{i} w^{T} x_{i}<0\right\}$$

无法直接对上市求导，因此可以间接通过 SGD 优化下面函数来求解：

$L(w)=\sum_{\left(x_{i}, y_{i}\right) \in D}-y_{i} w^{T} x_{i}$

逻辑回归

逻辑回归可以理解为：激活函数使用了 sigmoid 的线性回归。

为什么选 sigmoid

逻辑回归不能使用平方损失的其中一个原因是，MSE 的梯度为：$\frac{\partial}{\partial \theta_{j}} j(\theta)=(z(x)-y) \cdot z^{\prime}(x) \cdot x_{j}$ 当误差越大，更新越小，与我们的期望不符。相比较交叉熵的梯度：$\left.=-1 / m \sum_{i=1}^{m}\left(y i-h_{\theta}(x i)\right) x i_{j}\right)$

逻辑回归，线性回归均属于 Generalized Linear Model。考虑一个分类或回归问题，GLM 有以下三个假设：

• $p(y|x;\Theta)$ 服从指数族分布
• 给定 x，问题的目的是预测 $T(y)$ 在条件 x 下的期望
• 指数族分布的参数 $\eta =\Theta^TX$

因为是二分类问题，假设 $P(Y|X,\Theta)$服从伯努里分布，因此：

$$\begin{aligned} h_{\theta}(x) &=E[y \mid x ; \theta] \\ &=\phi \\ =& \frac{1}{1+e^{-\eta}} \\ =& \frac{1}{1+e^{-\theta^{T} x}} \end{aligned}$$

指数族分布

$$p(y ; \eta)=b(y) \exp \left(\eta^{T} T(y)-a(\eta)\right)$$

伯努利的指数族分布形式：

$$\begin{array}{c} p(y ; \phi)=\phi^{y}(1-\phi)^{1-y} \\ =\exp [y \log \phi+(1-y) \log (1-\phi)] \\ =\exp \left[y \log \frac{\phi}{1-\phi}+\log (1-\phi)\right] \end{array}$$

所以

$$\eta=\log \frac {\phi}{1-\phi}$$

使用 MLE 求解最优参数：

$$\begin{aligned} \hat{w} &=\underset{w}{\operatorname{argmax}} \log (P(Y \mid X)) \\ &=\underset{w}{\operatorname{argmax}} \log \left(\prod_{i=1}^{N} P\left(y_{i} \mid x_{i}\right)\right) \\ &=\underset{w}{\operatorname{argmax}} \sum_{i=1}^{N} \log \left(P\left(y_{i} \mid x_{i}\right)\right) \\ &=\underset{w}{\operatorname{argmax}} \sum_{i=1}^{N} \log \left(p_{1}^{y_{i}} \cdot p_{0}^{1-y_{i}}\right) \\ &=\operatorname{argmax} \sum_{w}^{N}\left(y_{i} \log p_{1}+\left(1-y_{i}\right) \log p_{0}\right) \end{aligned}$$

此处 $y_{i} \log p_{1}+\left(1-y_{i}\right) \log p_{0}$ 为负的交叉熵。 因此最小化交叉熵与 MLE 是等价的。

由于概率的非线性，在实际训练中，采用梯度下降或拟牛顿法来进行优化。

朴素贝叶斯

为简化运算，提出了条件独立假设：$x_{i} \perp x_{j} \mid y(i \neq j)$