Aho-Corasick 多字符串匹配算法

Kevin 吴嘉文大约 5 分钟

Aho-Corasick 多字符串匹配加速算法。文章包括 Tire, KMP, Aho-Corasick

需要匹配的单词有 n 个，要在一篇具有 m 个单词的文章中找出他们的位置。

AC 自动机可以理解为 Tire 与 KMP 算法的结合。使用 fail 指针加速了字符串匹配的速度。

Trie

前缀树/字典树的插入、查询时间复杂度均为为 $O(|S|)$ ，其中 $|S|$ 是每次插入或查询的字符串的长度。空间复杂度为 $O(|T|·\sum)$ 其中 $|T|$ 为插入字符串长度之和， $\sum$ 为字符集大小。

class Trie {
private:
    vector<Trie*> children;
    bool isEnd;
    Trie* searchPrefix(string prefix) {
        Trie* node = this;
        for (char ch : prefix) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                return nullptr;
            }
            node = node->children[ch];
        }
        return node;
    }

public:
    Trie() : children(26), isEnd(false) {}

    void insert(string word) {
        Trie* node = this;
        for (char ch : word) {
            ch -= 'a';
            if (node->children[ch] == nullptr) {
                node->children[ch] = new Trie();
            }
            node = node->children[ch];
        }
        node->isEnd = true;
    }

    bool search(string word) {
        Trie* node = this->searchPrefix(word);
        return node != nullptr && node->isEnd;
    }

    bool startsWith(string prefix) {
        return this->searchPrefix(prefix) != nullptr;
    }
};

KMP

力扣实现 strstr()open in new window KMP 算法详解（另类 KMP）open in new window 如何更好地理解和掌握 KMP 算法?open in new window

从长度 m 的字符串中匹配出长度为 n 的字符串。时间复杂度 $O(m+n)$

首先需要求 next 数组算法open in new window。字符串 A 对应的 next 数组为 pmt 数组右移一位得到，next=pmt>>1; pmt[i] 表示 A[0:pmt[i]] = A[pmt[i]:i]

void getNext(char * p, int * next)
{
	next[0] = -1;
	int i = 0, j = -1;

	while (i < (int)strlen(p))
	{
		if (j == -1 || p[i] == p[j])
		{
			++i;
			++j;
			next[i] = j;
		}	
		else
			j = next[j];
	}
}

利用 next 数组，在匹配失败的时候只需要将指针 j 移动到 next[j] 的位置然后继续匹配，i 指针不需要回溯。

int KMP(char * t, char * p) 
{
	int i = 0; 
	int j = 0;
	while (i < (int)strlen(t) && j < (int)strlen(p))
	{
		if (j == -1 || t[i] == p[j]) 
		{
			i++;
           		j++;
		}
	 	else 
           		j = next[j];
    	}

    if (j == strlen(p))
       return i - j;
    else 
       return -1;
}

AC 自动机

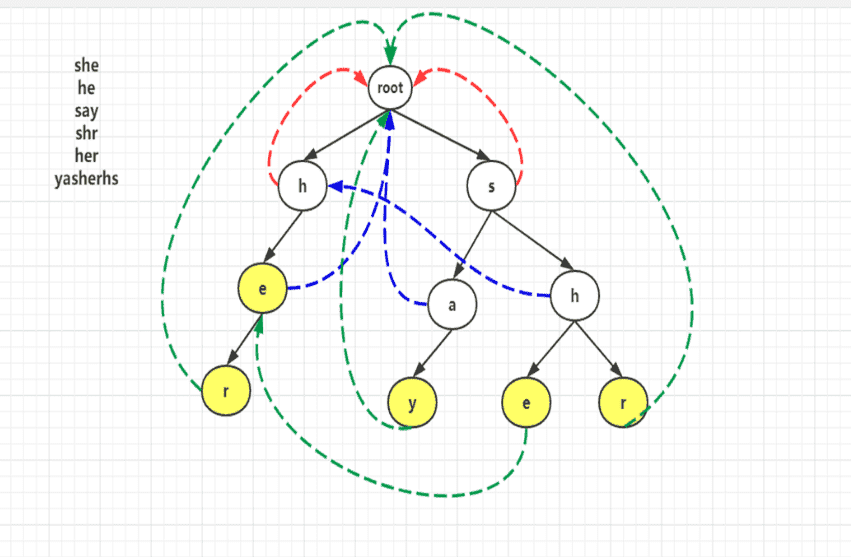
参考 KMP 的思想，我们将待匹配字符串储存为 Trie 树，而后添加 fail 指针来减少回溯匹配浪费的时间。（该部分参考自：AC 自动机算法详解open in new window）

fail 指针的用途：

参考上图例子，需要匹配的字符串有：{"str","she","say","her"} ，假设主字符串为："should" 。首先匹配 "str"，在匹配第二个字符 'h' 时成功，接着匹配他的子节点，匹配到第 3 个字符（'r'!='o'）时失败，而后匹配 'e'!='o'也失败，此时跳转到 h fail 指针对应地址继续匹配，即匹配 he 与 ho。

fail 指针的构建：

Fail 指针用 BFS 来求得，对于直接与根节点相连的节点来说，如果这些节点失配，他们的 Fail 指针直接指向 root 即可，其他节点其 Fail 指针求法如下：假设当前节点为 father，其孩子节点记为 child。求 child 的 Fail 指针时，首先我们要找到其 father 的 Fail 指针所指向的节点,假如是 t 的话，我们就要看 t 的孩子中有没有和 child 节点所表示的字母相同的节点，如果有的话，这个节点就是 child 的 fail 指针，如果发现没有，则需要找 father->fail->fail 这个节点，然后重复上面过程，如果一直找都找不到，则 child 的 Fail 指针就要指向 root。

代码

root 节点结构

const int kind = 26; 
struct node
{
    node *fail;       //失败指针
    node *next[kind]; //Tire 每个节点的个子节点（最多个字母）
    int count;        //是否为该单词的最后一个节点
    node()            //构造函数初始化
    {
        fail=NULL;
        count=0;
        memset(next,NULL,sizeof(next));
    }
}*q[500001];          //队列，方便用于 bfs 构造失败指针
char keyword[51];     //输入的单词
char str[1000001];    //模式串
int head,tail;        //队列的头尾指针

插入

void insert(char *str,node *root){ 
    node *p=root;
    int i=0,index;
    while(str[i])
    {
        index=str[i]-'a';
        if(p->next[index]==NULL) p->next[index]=new node();
        p=p->next[index];
        i++;
    }
    p->count++;     //在单词的最后一个节点 count+1，代表一个单词
}

构建 fail 指针

 void build_ac_automation(node *root){
    int i;
    root->fail=NULL;
    q[head++]=root;
    while(head!=tail)
    {
        node *temp=q[tail++];
        node *p=NULL;
        for(i=0; i<26; i++)
        {
            if(temp->next[i]!=NULL)
            {
                if(temp==root) temp->next[i]->fail=root;
                else
                {
                    p=temp->fail;
                    while(p!=NULL)
                    {
                        if(p->next[i]!=NULL)
                        {
                            temp->next[i]->fail=p->next[i];
                            break;
                        }
                        p=p->fail;
                    }
                    if(p==NULL) temp->next[i]->fail=root;
                }
                q[head++]=temp->next[i];
            }
        }
    }
}

字符串匹配

 int query(node *root){ 
    int i=0,cnt=0,index,len=strlen(str);
    node *p=root;
    while(str[i])
    {
        index=str[i]-'a';
        while(p->next[index]==NULL && p!=root) p=p->fail;
        p=p->next[index];
        p=(p==NULL)?root:p;
        node *temp=p;
        while(temp!=root && temp->count!=-1)
        {
            cnt+=temp->count;
            temp->count=-1;
            temp=temp->fail;
        }
        i++;
    }
    return cnt;
}

pyahocorasick

python 下的 AC 自动机库 pip install pyahocorasick 官方文档open in new window

构建

import ahocorasick
actree = ahocorasick.Automaton()  # use the Automaton class as a trie
for index, word in enumerate(wordlist):
    actree.add_word(word, (index, word))
actree.make_automaton()  # convert the trie to an Aho-Corasick automaton to enable Aho-Corasick search

# 'word' in actree 检查字符是否在 trie 中

查询使用 actree.iter(string) ，返回结果为 匹配到单词时结束的位置、构建时候插入的 index、匹配到的单词

>>> for end_index, (insert_order, original_value) in A.iter(haystack):
...     start_index = end_index - len(original_value) + 1
...     print((start_index, end_index, (insert_order, original_value)))
...     assert haystack[start_index:start_index + len(original_value)] == original_value
...
(1, 2, (0, 'he'))
(1, 3, (1, 'her'))

保存与加载

import cPickle
pickled = cPickle.dumps(A)
B = cPickle.loads(pickled)
B.get('he')

Aho-Corasick 多字符串匹配算法

# Trie

# KMP

# AC 自动机

# 代码

# pyahocorasick

Trie

KMP

AC 自动机

代码

pyahocorasick