对话系统笔记（一）|检索基础

Kevin 吴嘉文大约 12 分钟

本文为文本距离（WMD，BM25），检索（倒排索引），邻近搜索（ Annoy, KD tree, HNSW ）的一些基础方法进行了笔记梳理。

检索式对话系统基础

文本表征的一些方法

句向量： 词向量求平均，将 tf-idf 当做单词权重，或者使用 SIF 加权平均（效果似乎更好）。

中文词向量链接：github.com/Embedding/Chinese-Word-Vectors
quick-Thought Vectors
- 使用孪生网络，与问答查重理论相同。或者输入输出使用不同的 encoder，使用负采样，负采样为预料中上下文的句子，和词向量的负采样原理相似。

tf-idf

tf-idf 是常用的文本表征方法，主要思想是以下公式：

\begin{gathered} TFI D F=T F(t, d) \times I D F(t) \\ T F(t, d)=\# \mathrm{t} \text { 在文档 } \mathrm{d} \text { 中出现的次数 } \\ I D F(t)=\log \frac{k+|D|}{k+\left|j: t_{i} \in d_{j}\right|}+1=\log \frac{k+\text { 包含单词 } t \text { 的文档数量 }}{k+\text { 包含单词 t 的文档数量 }}+1 \end{gathered}

其中， $k$ 为朝参，用于控制句子表征分布的平滑程度，通常为 1（当然很多地方只对分母添加平滑因子）。此外， TF 项也能够进行归一化，常见的归一化方案如，除以文档全部单词数量等。

以 sklearn 为例，sklearn 中采用 k==int(smooth_idf) 进行平滑控制。采用 l1 或 l2 来进行归一化。如何配置 TF-IDF 的超惨，也成为了一个玄学。

SIF

文本距离（文本相似度）

WMD

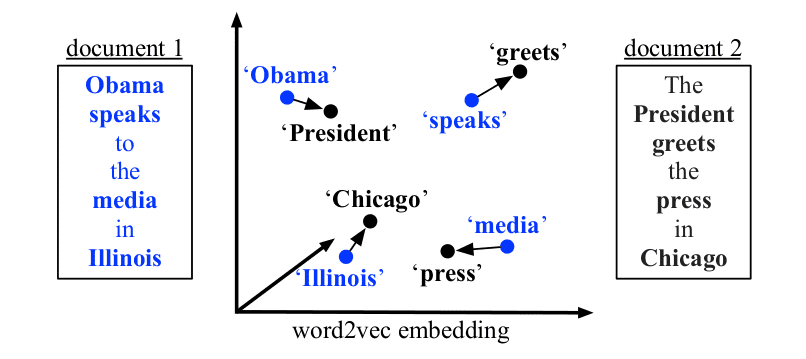
求句子转换之间最小的距离（将句子 A 中的每个词通过词向量移动，转换成为句子 B 的最小总距离。）。WMD 的计算依赖于单词词向量，加入我们基于 Word2vec 来计算 WMD，那么可能需要进行停用词去除等 Word2Vec 需要的操作。一些缺点是：WMD 只考虑可一一对应关系，没有考虑词与词之间多多对应的关系。网友论文笔记open in new window

\begin{aligned} \min _{\mathbf{T} \geq 0} & \sum_{i, j=1}^{n} \mathbf{T}_{i j} c(i, j) \\ \text { subject to: } & \sum_{j=1}^{n} \mathbf{T}_{i j}=d_{i} \quad \forall i \in\{1, \ldots, n\} \\ & \sum_{i=1}^{n} \mathbf{T}_{i j}=d_{j}^{\prime} \quad \forall j \in\{1, \ldots, n\} . \end{aligned}

d_{i}=\frac{c_{i}}{\sum_{j=1}^{n} c_{j}}

其中， $d_i$ 为一个文档中第 i 个词的 nBOW（Normalized Bag-of-words）表示。 $c_i$ 为该词在该文档中出现次数。

优化方案：

Word centroid distance

\begin{aligned} & \sum_{i, j=1}^{n} \mathbf{T}_{i j} c(i, j)=\sum_{i, j=1}^{n} \mathbf{T}_{i j}\left\|\mathbf{x}_{i}-\mathbf{x}_{j}^{\prime}\right\|_{2} \\ =& \sum_{i, j=1}^{n}\left\|\mathbf{T}_{i j}\left(\mathbf{x}_{i}-\mathbf{x}_{j}^{\prime}\right)\right\|_{2} \geq\left\|\sum_{i, j=1}^{n} \mathbf{T}_{i j}\left(\mathbf{x}_{i}-\mathbf{x}_{j}^{\prime}\right)\right\|_{2} \\ =&\left\|\sum_{i=1}^{n}\left(\sum_{j=1}^{n} \mathbf{T}_{i j}\right) \mathbf{x}_{i}-\sum_{j=1}^{n}\left(\sum_{i=1}^{n} \mathbf{T}_{i j}\right) \mathbf{x}_{j}^{\prime}\right\|_{2} \\ =&\left\|\sum_{i=1}^{n} d_{i} \mathbf{x}_{i}-\sum_{j=1}^{n} d_{j}^{\prime} \mathbf{x}_{j}^{\prime}\right\|_{2}=\left\|\mathbf{X} \mathbf{d}-\mathbf{X} \mathbf{d}^{\prime}\right\|_{2} \end{aligned}

通过两个文档词向量中心的距离来计算文档距离下限。

relaxed word moving distance

保留 WMD 其中一个限定条件

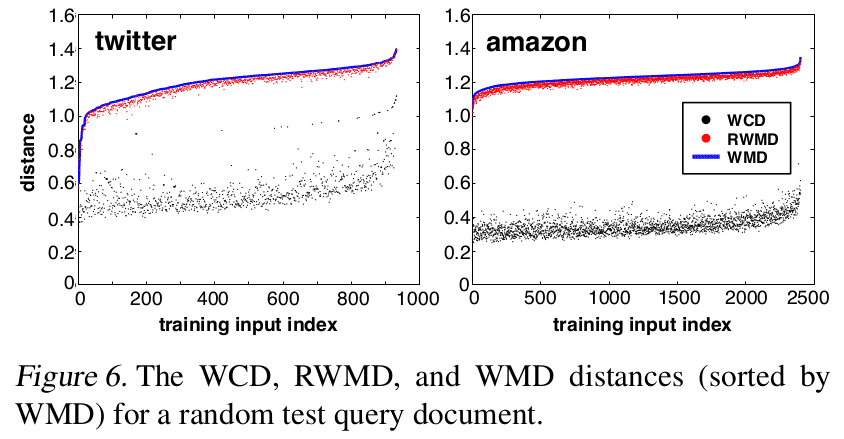
实验表现 WCD 求得的边界比 RWMD 差距更大。

通过 WMD 计算 KNN 时候，可以用 WCD 进行粗排，而后进行精排

代码：gensim

from gensim.similarities import WmdSimilarity

class WMDRetrievalModel:

    def __init__(self,corpus,gensim_model_path):
        Word2Vec_model = Word2Vec.load(gensim_model_path)
        self.wmd_similarity  = WmdSimilarity(corpus,Word2Vec_model)

    def get_top_similarities(self,query,topk=10):
        sims = self.wmd_similarity[query][0:topk]
        return sims[0][0],sims[1][0]

BM25

网友文档 - 附解释代码open in new window

用来评价搜索词和文档词之间的相关性的算法，基于概率检索模型提出，可以用来做召回

query $Q$ 与文档 $d$ 评分计算方式：

$Score(Q, d) = \sum W_iR(q_i,d)$

将 $Q$ 切分为单词 $q_i$
每个单词对应权重 $W_i = IDF(q_i)=\log \frac{N}{\sum_{n\in N} n(q_i)+1}$ , $n(q_i)=1$ 表示文档 $n$ 包含 $q_i$ 这个词， $N$ 表示文档总数
单词 $q$ 与文档 $d$ 相关性 $R()$ 的计算： $f_i$ 为 t 在文档 $d$ 中的词频， $qf_i$ 为 $q_i$ 在 query 中的词频。 $dl$ =当前 doc 长度 $k_1,k_2,b$ 是超参，通常为 $1,2,0.75$ 。

\begin{aligned} R\left(q_{i}, d\right) &=\frac{f_{i} \cdot\left(k_{1}+1\right)}{f_{i}+K} \cdot \frac{q f_{i} \cdot\left(k_{2}+1\right)}{q f_{i}+k_{2}} \\ K &=k 1 \cdot\left(1-b+b \cdot \frac{d l}{a v g d l}\right) \end{aligned}

K 越大表示 d 文档的长度越长，所包含的信息可能就越多。

k1 越大，我们越看重单词在文档 d 中词频的影响。k2 越大，越看重单词在 query 中的词频。

class BM25(object):
    def __init__(self,
                 do_train=True,
                 save_path=os.path.join(root_path, 'model/ranking/')):
        if do_train:
            self.data = pd.read_csv()
            self.idf, self.avgdl = self.get_idf()
            self.saver(save_path)
        else:
            self.stopwords = self.load_stop_word()
            self.load(save_path)

    def load_stop_word(self):
        return stopwords

    def n_containing(self, word, count_list):
        return sum(1 for count in count_list if word in count)

    def cal_idf(self, word, count_list):
        """
        count_list (list[string]): The corpus, list of document strings.
        """
        return math.log(
            len(count_list)) / (1 + self.n_containing(word, count_list))

    def get_idf(self):
        self.data['question2'] = self.data['question2'].apply(
            lambda x: ' '.join(jieba.cut(x)))
        idf = Counter(
            [y for x in self.data['question2'].tolist() for y in x.split()])
        idf = {
            k: self.cal_idf(k, self.data['question2'].tolist())
            for k, v in idf.items()
        }
        avgdl = np.array(
            [len(x.split()) for x in self.data['question2'].tolist()]).mean()
        return idf, avgdl

    def saver(self, save_path):
        joblib.dump(self.idf, save_path + 'bm25_idf.bin')
        joblib.dump(self.avgdl, save_path + 'bm25_avgdl.bin')

    def load(self, save_path):
        self.idf = joblib.load(save_path + 'bm25_idf.bin')
        self.avgdl = joblib.load(save_path + 'bm25_avgdl.bin')

    def bm_25(self, q, d, k1=1.2, k2=200, b=0.75):
        """
        Compute bm25 score.
        Args:
            q (str): query text.
            d (str): document content.
            k1 (float, optional):
                control the importance of frequency in the query.
            k2 (float, optional):
                control the importance of frequency in the document.
            b (float, optional):
                factor to control relative document length.
        """
        stop_flag = ['x', 'c', 'u', 'd', 'p', 't', 'uj', 'm', 'f', 'r']
        words = pseg.cut(q)  # 切分查询式
        fi = {}
        qfi = {}
        for word, flag in words:
            if flag not in stop_flag and word not in self.stopwords:
                fi[word] = d.count(word)
                qfi[word] = q.count(word)
        K = k1 * (1 - b + b * (len(d) / self.avgdl))
        ri = {}
        for key in fi:
            ri[key] = fi[key] * (k1 + 1) * qfi[key] * (k2 + 1) / (
                (fi[key] + K) * (qfi[key] + k2))  # 计算 R

        score = 0
        for key in ri:
            score += self.idf.get(key, 20.0) * ri[key]
        return score

检索 Information Retrieval

用空间换时间复杂度

倒排索引

网文open in new window

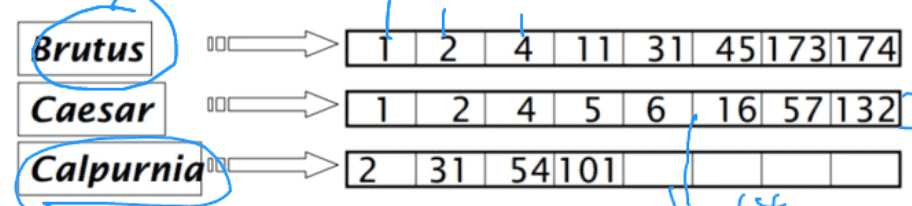
倒排索引：对每一个词项（搜索项），储存包含这个词的文档的一个列表，或者是链表。

建立步骤

文本词条化
按照文档 id 顺序，建立词条序列（储存搜索词与对应文档 id 的数据对）
按词条排序，然后按文档 ID 排序（这样查询 A && B 的时候就可以使用双指针对 A，B 的文档列表进行遍历了。）

空间优化方法 Variable Byte Compression

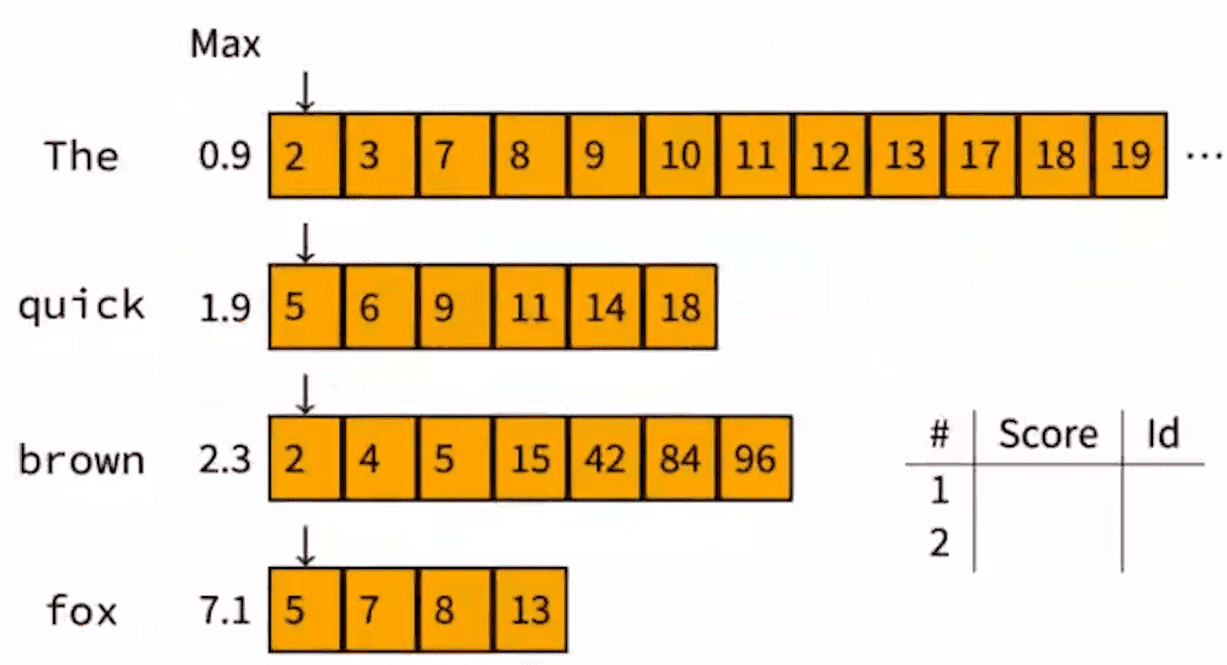
优化长 query: Wand

问题描述：
- 转出与 query 相关的 topK 个文档
对 query 进行切分
计算每个词在对应文档索引的最大贡献值（tf-idf）
根据每个分词建立滑动指针，从小到大遍历文档，记录文档对应 query 最大的 tf-idf。如果计算某文档时候，所有分词对应的最大贡献无法超过当前 query 最大贡献，则跳过该文档的贡献值计算。

邻近搜索

Annoy

Spotify 开源的高维空间近似最近邻库，通过对表征空间多次划分来建立二叉树。

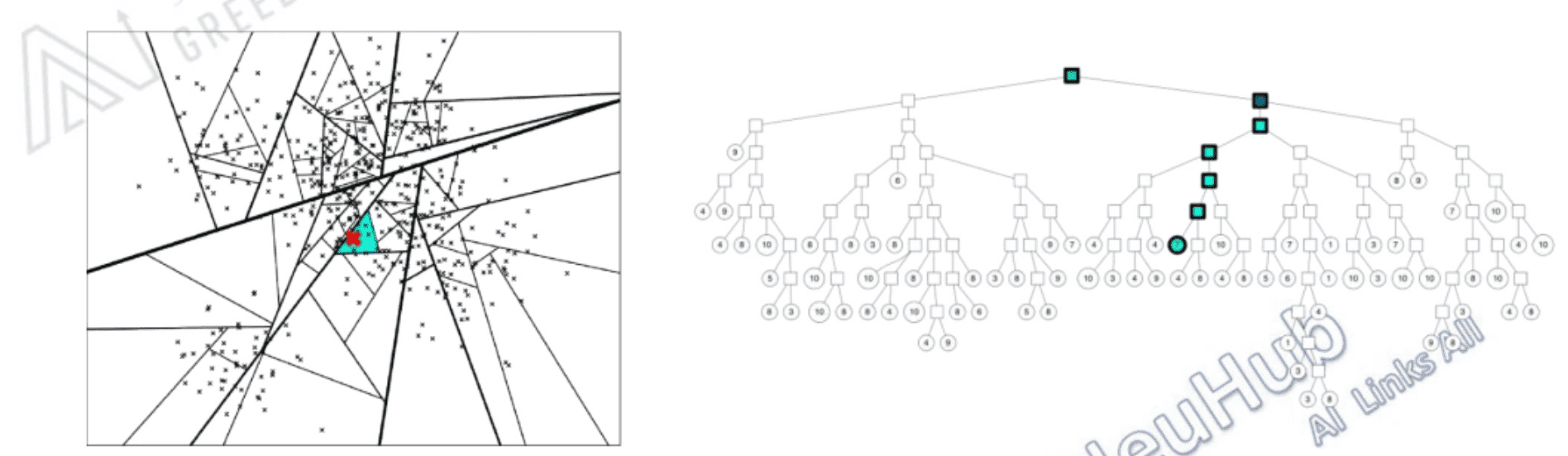
首先假设我们已经有了表征

中文词向量 Tencent_AILab_Chines

建立成二叉树

随机选两点，根据两点链接的法线进行空间切分
重复上述操作。
终止条件：总空间数或各空间节点数。

遍历二叉树

根据我们划分二叉树的方法，一个节点就是一条空间划分线，样本与空间划分线点积得到正负，即为他们的相对位置。
若使用一棵树，要寻找进行更准确的查找：
- 找最近划分线对应节点。
- 对划分线两边都进行遍历
或建立多颗树，进行更精确的查找。

HNSW

网友：HNSW 学习笔记open in new window，HNSW 的基本原理及使用open in new window，近似最近邻算法 HNSW 学习笔记open in new window，一文看懂 HNSW 算法理论的来龙去脉open in new window。代码：HNSW demosopen in new window

NSW

查询方式：

K-NNSearch(object q,integer:m,k)
  TreeSet[object]tempRes, candidates, visitedSet, result
   for(i<-0; i<m; i++) do:
    put random entry point in candidates
    tempRes<-null
    repeat:
     get element c closest from candidates to q
     remove c from candidates
    #checks to p condition:
    if c is further than k-th element from result
     than break repeat
     #update list of candidates:
     for every element e from friends of c do:
      if e is not in visited Set than
       add e to visited Set, candidates, tempRes
  
     end repeat
     #aggregate the results:
     add objects from tempRes to result
    end for
    return best k elements from result

图构建

构建图的时候，理论上来说我们对所有的点做 Delaunay 三角剖分，然后添加一些随机的长边构建快速检索通道，就构建了一个可导航的小世界网络。

由于构建 Delaunay 三角剖分的复杂度太高实际的代码实现过程中是通过节点随机插入来引入随机性，利用已有节点构建 Delaunay 边来引入同质性。

NSW 的网络构建过程如下:

向图中插入新点时，通过随机存在的一个点出发，查找距离新点最近的 m 个点并连接。而后更新插入点周边点信息，删除被连接节点多余的链接。
查询时间复杂度高

HNSW = NSW + SKIP LIST，利用 skip list 思想，插入与查询时间减少为 O(log n) 用于理解的 python 代码open in new window

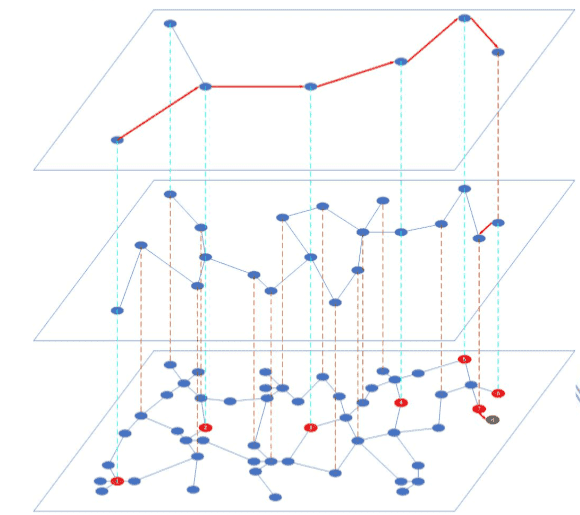
构建时候的参数：

M - 插入新点时候，需要添加的双向链接的数量。

$M_{max}$ - 插入点时候，每个点限制拥有的最多链接熟练量。

ef-construct：搜索时候的动态列表大小，影响到算法速度。

插入点算法：

使用大小为 ef 的动态列表进行搜索，搜索 k 个邻居点。计算第 0 层每个点可以深入到第 $l$ 层 $floor(-ln(uniform(0,1)))\times ml$ ，其中 ml 为超参。从 $l$ 层开始，每层需要找到 M 个邻居，然后进行链接。然后检查被链接的节点，如果他的链接数量超过了 $M_{max}$ ，需要对这个点重新分配邻居链接，保持链接数量不超过限制。ep - enter point 表示链接不同层的点。

查找某一层上节点 q 的 ef 个临近点算法

与 NSW 的搜索算法相似，使用 v （visited）, C （candidates）, 和 W （found Nearest neighbors）储存节点。只要 q 与 C 内点最短距离小于等于 q 与 W 内点最大距离，那么就对 C 集合中 节点的邻居节点 e 进行遍历，如果 e,q 距离小于 q 与 W 最大距离，就将 e 加入 C 和 W。

搜索点邻居算法

faiss 下 hnsw 的使用

建立数据结构

def build_hnsw(self, to_file, ef=2000, m=64):
    vecs = np.stack(self.data['custom_vec'].values).reshape(-1, 300)
    vecs = vecs.astype('float32')
    dim = self.w2v_model.vector_size

    index = faiss.IndexHNSWFlat(dim, m)
    index.hnsw.efConstruction = ef
    index.verbose = True
    index.add(vecs)
    faiss.write_index(index, to_file)  # 保存 hnsw 模型
    return index

指标评价模型 - 可以通过检索时间，recall@1（最近点应该是检索节点本身），和 missing rate 来判断

def evaluate(self, vecs, ground_truth):
    nq, d = vecs.shape
    t0 = time.time()
    p, i = self.index.search(vecs, 1)
    t1 = time.time()
    missing_rate = (i == -1).sum() / float(nq)
    recall_at_1 = (i == ground_truth).sum() / float(nq)
    print(f"\t {(t1 - t0) * 1000 / nq:.3f} ms per query, "
          f"Recall@1 {recall_at_1:.4f}, "
          f"missing_rate {missing_rate:.4f}")

加载 HNSW

def load_hnsw(self, model_path):
    logging.info(f'Loading hnsw index from {model_path}.')
    hnsw = faiss.read_index(model_path)
    return hnsw

检索

def search(self, text, k=5):
    logging.info(f"Searching for {text}.")
    test_vec = wam(clean(text), self.w2v_model)
    D, i = self.index.search(test_vec, k)
    result = pd.concat(
        (self.data.iloc[i[0]]['custom'].reset_index(),
         self.data.iloc[i[0]]['assistance'].reset_index(drop=True),
         pd.DataFrame(D.reshape(-1, 1), columns=['q_distance']))
        , axis=int)
    return result

案例

hnsw = HNSW(config.w2v_path,
            config.ef_construction,
            config.M,
            config.hnsw_path,
            config.train_path)
test = '转人工'
print("test:\n", hnsw.search(test, k=10))
eval_vecs = np.stack(hnsw.data['custom_vec'].values).reshape(-1, 300)
eval_vecs.astype('float32')
hnsw.evaluate(eval_vecs[:10000],
              ground_truth=np.arange(10000))

KD Tree

网友笔记open in new window（其他相关树 R-TREE, BALL-TREE）

构建树

取方差最大维度的特征作为分割特征，取特征的中间值作为分类点进行二分划分。直到每个空间只有一个点。
在最后一次搜索中，根据搜索点与最后二分节点作为半径画圆，与其他切分线有相交的话，需要回溯。计算相交切分线另一边空间。

邻居点搜索

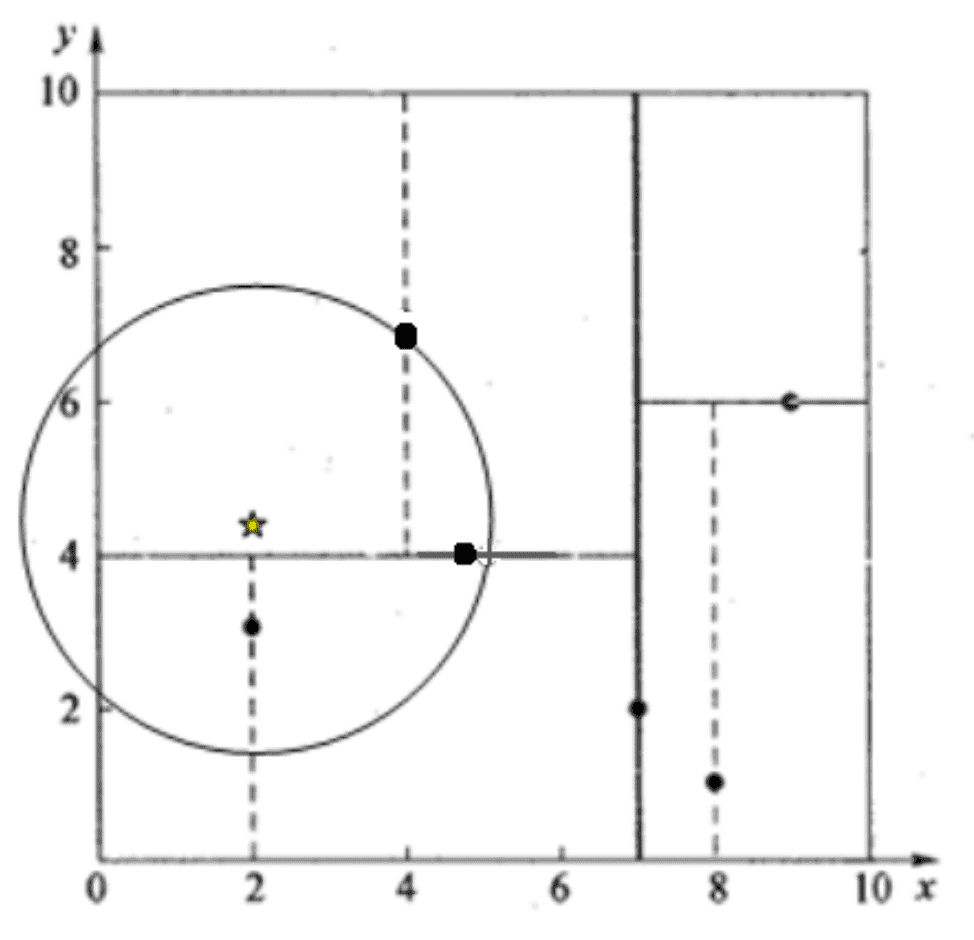
通过二叉树搜索进行查找可能会漏掉准确值，因此我们需要进行回溯。查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后 search_path 中的结点为<(7,2), (5,4), (4,7)>，从 search_path 中取出(4,7)作为当前最佳结点 nearest, dist 为 3.202；然后回溯至(5,4)，以(2,4.5)为圆心，以 dist=3.202 为半径画一个圆与超平面 y=4 相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到 search_path 中，现在 search_path 中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为 3.04 < dist = 3.202，所以将(5,4)赋给 nearest，并且 dist=3.04。回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为 1.5，所以 nearest 更新为(2,3)，dist 更新为(1.5) 回溯至(7,2)，同理，以(2,4.5)为圆心，以 dist=1.5 为半径画一个圆并不和超平面 x=7 相交, 所以不用跳到结点(7,2)的右子空间去搜索。至此，search_path 为空，结束整个搜索，返回 nearest(2,3)作为(2,4.5)的最近邻点，最近距离为 1.5。 ———————————————— 引用于CSDN - 详解 KDTreeopen in new window

其他

LSH Locality Sensitive Hashing
min-hashing：每一列的第一个 1 出现的位置。最小哈希相等的概率和 jaccard 相似度的概率一样。
最小签名表
文本的相似度和他们出现在同一个桶中的概率相似。

对话系统笔记（一）|检索基础

# 检索式对话系统基础

# 文本表征的一些方法

# 文本距离（文本相似度）

# WMD

# BM25

# 检索 Information Retrieval

# 倒排索引

# 优化长 query: Wand

# 邻近搜索

# Annoy

# HNSW

# faiss 下 hnsw 的使用

# KD Tree

# 其他