通俗易懂注意力机制
注意力机制有很多种,大致原理都是根据目标和输入的相似性来改进模型。不同模型的注意力机制假设与效果都不同。网上对于注意力机制的讲解很多,本文主要从相对小白的角度出发,谈谈笔者在学习注意力机制时的想法和总结,希望可以为刚入门的朋友们提供一些帮助。
文章知乎链接 知乎上的排版更好哈!
注意力机制
注意力机制的主要思想是:我们通过输入或者输出,是否可以得到一些信息。这些信息让我们知道,哪部分输入更为重要。
我们通过 动手深度学习 中的一个例子来解释注意力的大致工作思想。来看下图:
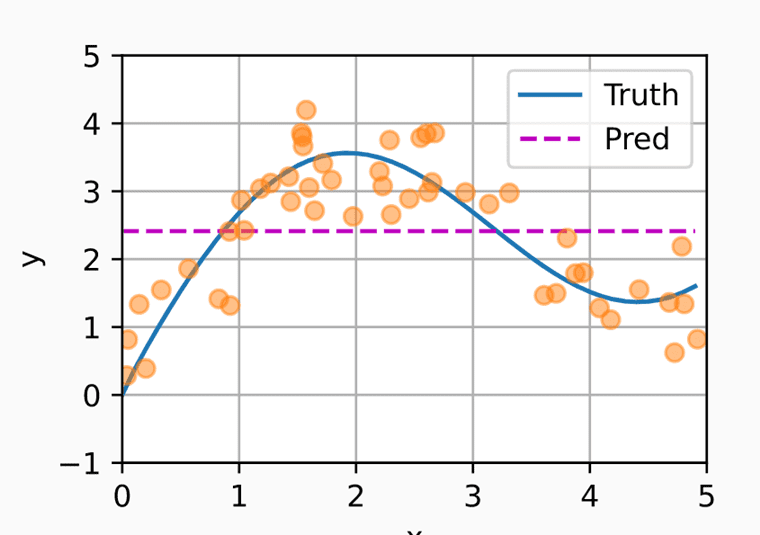
假设橙色点为我们已有数据集,蓝色曲线为 是我们想要求的 ground truth。
如果我们使用样本 的均值作为预测值,那么就有了紫色虚线。显然我们的预测很差。
没有参数的注意力池化 attention pooling
一个改进的方法是:我们根据输入 x 的位置,来给我们的输出 y 加上对应的权重。如下:
其中 是核方程,类似与 SVM 中的 。上面的方程也可以写成:
其中, 就是我们要给对应 加上的权重。这时,我们考虑使用 Gaussian kernel。
那么我们的预测函数 就变成了:
这时候,我们通过方程可以清晰得理解到,当我们索要 对应的 值时, 会与所有的 计算并得到权重, 与 越相似时,我们给到对应的 权重就越大,可以说我们使用了 的位置信息进行预测。二者上边的 也分别对应注意力机制中的 Query, Key, Value。通常每个 K 都会对应一个 V。
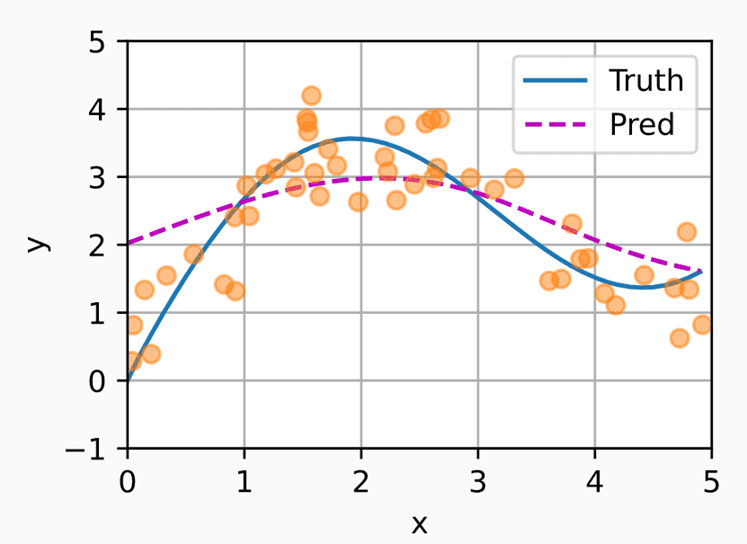
可以看到,在加上了没有参数的注意力池化之后,预测效果更好了。
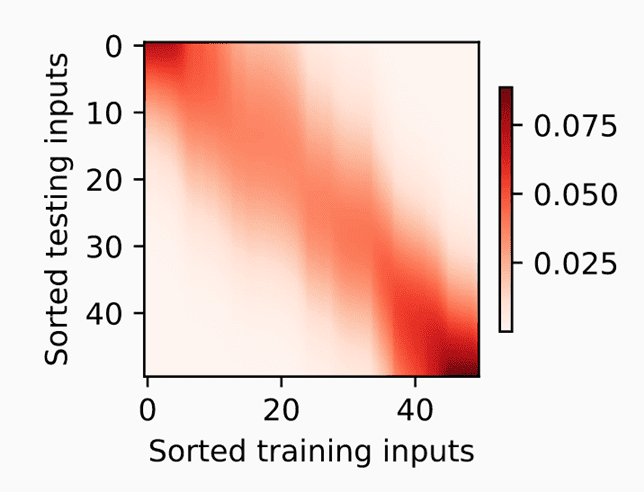
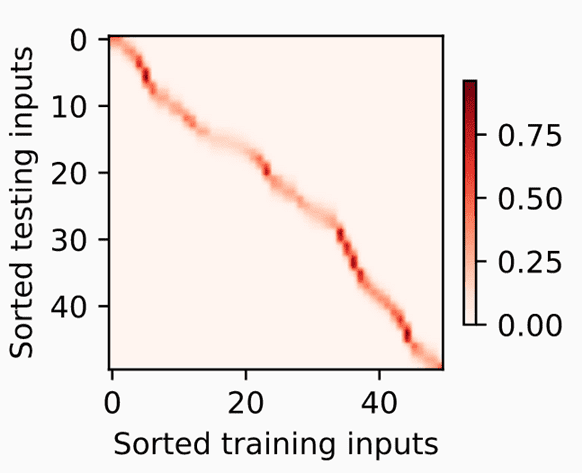
上图展示了输入 和训练集 之间的关系。
总结:通过 (Query) 和 (key) 计算对应的 权重。然后取 和作为我们的预测值。这种注意力机制一定程度上改善了我们的预测水平。
有参数的注意力池化
将我们的 通过可训练矩阵 投影之后再取 softmax,即换个角度来看 Query 和 Key 之间的关系。 更改后的方程如下:
在训练之后,效果比无参数的注意力池化更明显了,不过在这个例子中有些过拟合。
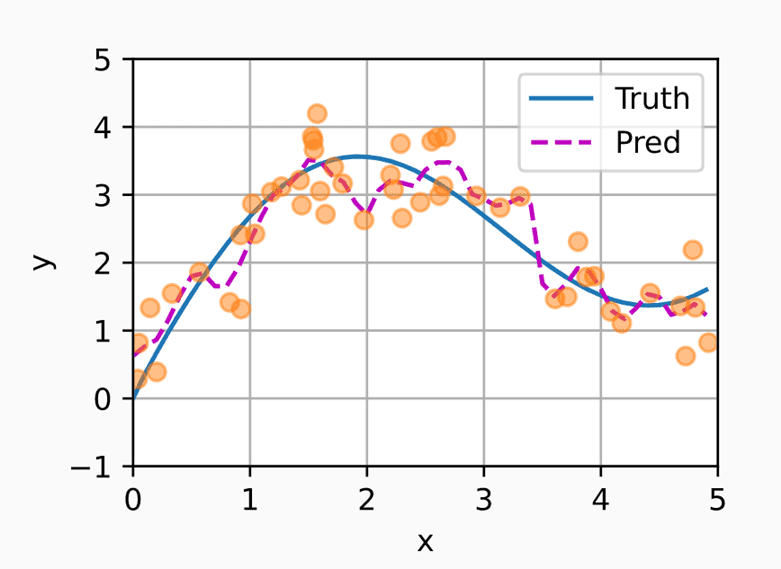
可以看到,还了一个观察角度。我们的注意力更集中了。
从上面两个例子可以看出,
- 注意力池化可以是有参数或者无参数的
- 在注意力池化中,每个 Value 都会被分配一个权重
注意力评分方程
通过上面的例题,你应该可以理解下面的这个式子:
其中 q, k 和 v 分别代表 query,key 和 value。其中的 经常是 softmax 形式的函数:
那么,一个问题来了,我们应该怎么去选择公式 中的方程 呢?
Masked Softmax
我们通常会将句子进行 padding,填充以使每个 batch 中的句子长度相同,提升训练速度,因此需要将被填充的部分进行掩盖。
一个 mask 的方式就是将需要掩盖的部分加上 M,如针对tensor([10,10,2,2]),2 为 pading_token,进行掩码时加上M=tensor([0,0,1e-9,1e-9])那么 softmax 之后就可以得到 tensor([0.5,0.5,0,0]) 。
当然掩码还有其他的用途,如后面会介绍到的 transormer 就使用了掩码来将注意力锁定在目标前方序列中
加性注意力
想不到这个方法的直觉是啥。从一个角度看 query,然后从另一个角度看 key,然后从第三个角度看前两个角度看到的东西???

代码是最容易理解的语言:
class AdditiveAttention(nn.Module):
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
self.w_v = nn.Linear(num_hiddens, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
# 下面一步将 Q 和 K 分别对独自的 W 进行点乘
queries, keys = self.W_q(queries), self.W_k(keys)
# 输出的:queries[batch_size,num_qeury,num_hidden]
# 输出的:keys[batch_size,num_keys,num_hidden]
features = queries.unsqueeze(2) + keys.unsqueeze(1)
# broadcasting 相加,features[batch_size,num_qeury,num_keys,num_hidden]
features = torch.tanh(features)
scores = self.w_v(features).squeeze(-1)
# scores[batch_size,num_qeury,num_keys]
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
# value 的长度和 key 的长度是一样的。
Scaled Dot-Product Attention
这个方法的直觉就是相似性大的 q 和 k 他们之间的注意力就越大。一般来说,再算这个注意力前,输入和输出都是已经做过 layer normed 的了,所以点积相当于余弦相似度。
class DotProductAttention(nn.Module):
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
scores = torch.bmm(queries, keys.transpose(1, 2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
其他
除了上面两个之外,还有比较常用的 。解决的是 q 和 k 维度不匹配的问题。当然注意力模型都是可以根据脑洞自己设计的。
Multi-Head Attention
多头注意力最出名的便是 transformer 了,对于 transformer,后文也有解析。多头注意力的基本思想是:我们从 h 个不同的角度来观察 Q,K,V。观察的角度越多,获得的信息也就更全面,最后我们再把获得的全部信息拼接起来。
要从 h 个角度观察一个张量,即对张量做 h 次不同的映射。之后将 h 个注意力权重拼接得到最终注意力权重如下图:
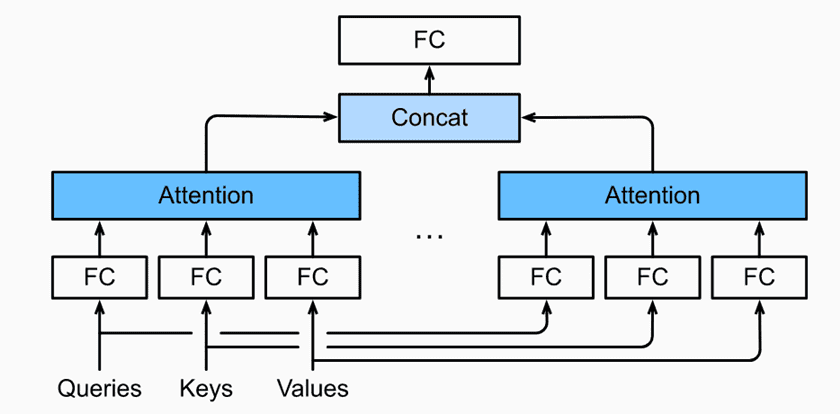
从以下代码可以看出,Q,K,V 三个张量在变化成多头前分别进行了矩阵映射。并且再映射后进行了掩码,valid_lens 就是 mask。
#@save
class MultiHeadAttention(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# Q,K,V [batch_size, len_seq, len_paris, d_model]
# valid_lens [batch_size,] or [batch_size, no. of queries]
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
# QKV [batch_size*num_head, len_sqe, d_model/num_head]
if valid_lens is not None:
valid_lens = torch.repeat_interleave(valid_lens,
repeats=self.num_heads,
dim=0)
output = self.attention(queries, keys, values, valid_lens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat) # [batch_size, len_seq, d_model]
案例 1:机械翻译
知识不懂,案例入手。
NMT 加入注意力之后表现更为优秀了,基于 RNN 的传统 seq2seq 模型有一个缺点便是信息瓶颈,即目标翻译句子的开始几个字将可以得到大部分的编码信息。随着翻译句子长度增加,后续的词解码时,hidden state 中保留的编码信息就越来越少。那么注意力机制可以解决这个问题吗?
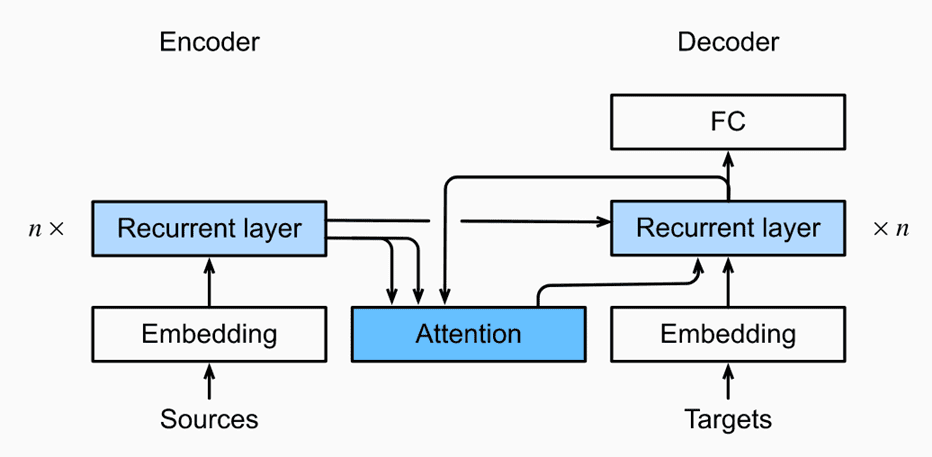
机械翻译中的注意力机制
先来看动手深度学习上的案例,我们再预测解码层的一个新字符时,都会使用上一个字符的 hidden state 作为 query 来计算注意力。显然,这里的假设就是:在机械翻译的过程中,一个字符的注意力权重可以使用相邻的字符特征来计算。下面的案例中使用的是加性注意力,而在 pytorch 的这份教程 中,模型使用的是乘积注意力。可以猜测 pytorch 的注意力模型假设相邻的字符拥有相似的特征,因此使用前一个字符的特征向量来计算当前字符的注意力权重可以起到一定的效果。
动手深度学习案例:
这个案例中的注意力放在了编码层和解码层中间,回想一下,我们的编码层通过编码输入的句子之后,最后一个 RNN 层将会有 cell state 和 1 个和 hidden state。而在下面这个机器翻译案例中,我们不难看出,它尝试将每一个解码层的输入和编码层中的所有输出进行注意力计算。这也使得在翻译句子后面的单词的时候,我们仍然可以通过调整注意力权重来使得目前翻译的单词使用到编码层前端的信息,从而解决了信息瓶颈问题。
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs): # num_hiddens 通常也就是我们词向量的维度了
super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
self.attention = d2l.AdditiveAttention(num_hiddens, num_hiddens,
num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,
dropout=dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
# Shape of `outputs`: (`num_steps`, `batch_size`, `num_hiddens`).
# Shape of `hidden_state[0]`: (`num_layers`, `batch_size`,
# `num_hiddens`)
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
# Shape of `enc_outputs`: (`batch_size`, `num_steps`, `num_hiddens`).
# Shape of `hidden_state[0]`: (`num_layers`, `batch_size`,
# `num_hiddens`)
enc_outputs, hidden_state, enc_valid_lens = state
# Shape of the output `X`: (`num_steps`, `batch_size`, `embed_size`)
X = self.embedding(X).permute(1, 0, 2)
outputs, self._attention_weights = [], []
for x in X:
# Shape of `query`: (`batch_size`, 1, `num_hiddens`)
query = torch.unsqueeze(hidden_state[-1], dim=1)
# Shape of `context`: (`batch_size`, 1, `num_hiddens`)
context = self.attention(query, enc_outputs, enc_outputs,
enc_valid_lens)
# Concatenate on the feature dimension
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# Reshape `x` as (1, `batch_size`, `embed_size` + `num_hiddens`)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [
enc_outputs, hidden_state, enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights
机械翻译的一些其他提示
当然注意力机制也只是机械翻译模型的成功的一个原因之一,因为懒得再另外写一篇 NMT 的博客了,这边就顺带分享一下一些机械翻译的学习心得吧。
数据处理
一般机械翻译任务的输入都是长度不固定的,这种情况下,我们通常使用 SGD。或者可以使用 bucketing 进行填充,填充后我们就可以打包 batch 并进行高效率的训练了。bucketing 的操作大致分为三布,首先将句子按照长短排序,然后将句子填充到最小的 长度。最后,把填充后长度相同的句子放进统一个 batch 训练,这时候就可以用上 Adam 等一些其他的优化器了。
Teacher forcing
应用 teacher forcing 效果更好,有老师监督的学习总是更高效 doge.jpg。Teacher forcing 的比率可以设置随着训练时间的增加而减少。
案例 2: Transformers
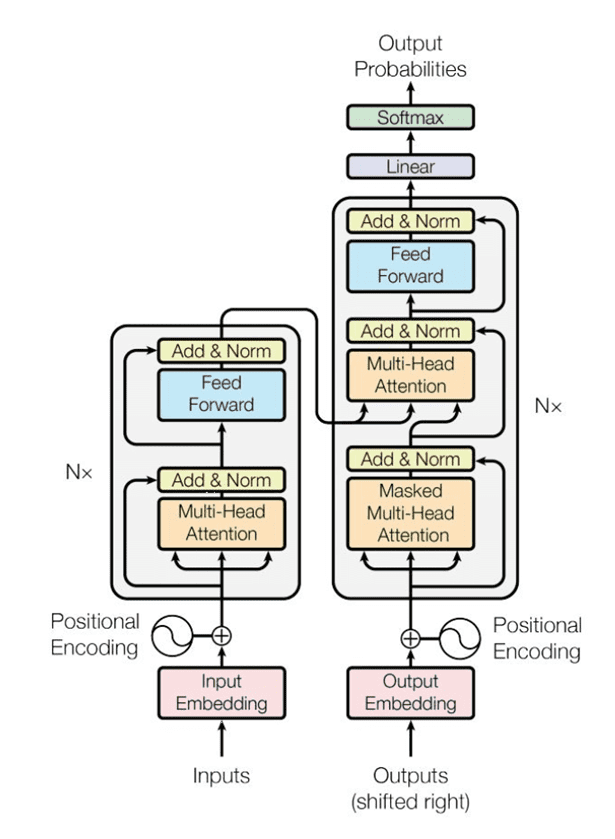
整个 transformer 分为 encoder 和 decoder,他们所使用的组件都大致相同。看上图,你可以这样理解:一种颜色的方框对应一种组件。接下来我们将重点介绍这些组件。
Positional Encoding
位置编码,即给词向量添加上这个词在句中位置的信息:
其中 是单词位置,i = (0,1,... d_model) 所以 d_model 为 512 情况下,第一个单词的位置编码可以表示为。
class PositionalEncoding(nn.Module):
def __init__(self, emb_size: int, dropout, maxlen: int = 5000):
super(PositionalEncoding, self).__init__()
den = torch.exp(- torch.arange(0, emb_size, 2) * math.log(10000) / emb_size)
pos = torch.arange(0, maxlen).reshape(maxlen, 1)
pos_embedding = torch.zeros((maxlen, emb_size))
pos_embedding[:, 0::2] = torch.sin(pos * den)
pos_embedding[:, 1::2] = torch.cos(pos * den)
pos_embedding = pos_embedding.unsqueeze(-2)
self.dropout = nn.Dropout(dropout)
self.register_buffer('pos_embedding', pos_embedding)
def forward(self, token_embedding: Tensor):
return self.dropout(token_embedding +
self.pos_embedding[:token_embedding.size(0),:])
此外,任意两个单词的位置编码信息是可以通过线性转换等到的。这使得来个相离很远的词也可以产生反映。
Scaled Dot-Product Attention
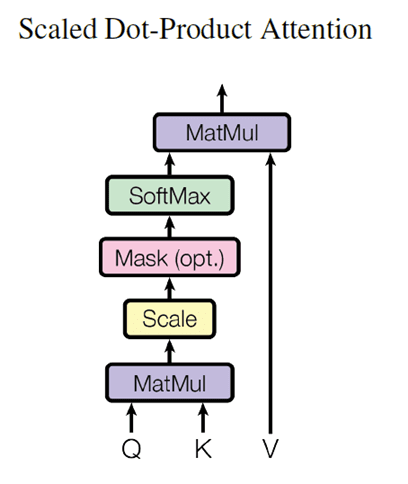
Scaled Dot-Product 的介绍是为 transformer 中的 multi-head attention 做铺垫。这个机制已经再文章前半部分介绍到,attention is all you need 文中指出,如果不进行归一化,那么会导致极其小的梯度。
下面是一个小小的测试,可以看出,当向量之间相似度越大,他们之间的注意力权重也就越大。
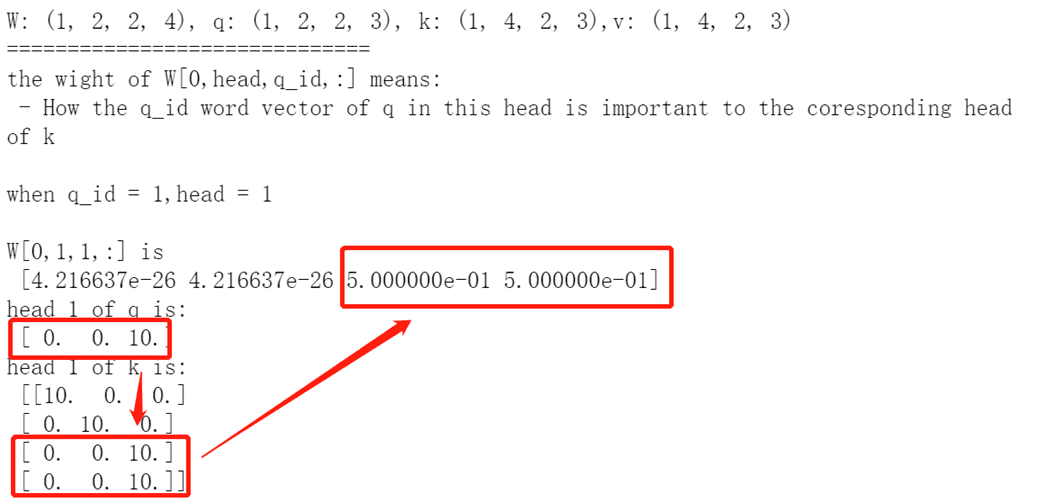
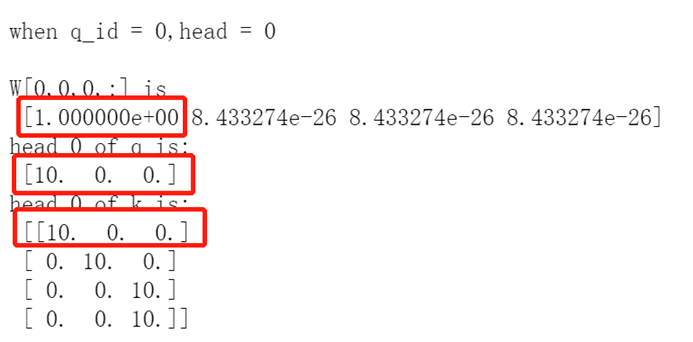
scaled dot product attention 假设我们再计算每层的注意力前,都进行了 layer norm。因此可以达到类似余弦相似度的效果。
Multi-head Attention
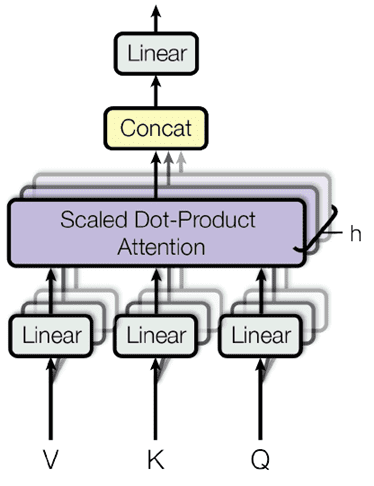
有了前面的 multi-head 铺垫,接下来让我们看看 Transformer 中是怎么设计的吧。
原文提到 V, K, 及 Q 再进行 Scaled Dot Product 前进行了映射,维度变成了: , 其中 h = 8 是个超参。单词的原维度为 512。这样做的直觉是:从不同的角度观察一组东西,你就能发现不同角度下他们的共同点,这边就是用了 8 个不同的角度去看。
Feed-Forward
一个简单的神经网络结构。
class PositionWiseFFN(nn.Module):
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
**kwargs):
super(PositionWiseFFN, self).__init__(**kwargs)
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
self.relu = nn.ReLU()
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
论文中使用的
Regularization
论文中只有两类情况使用了 dropout:
- 在每个 sub-layer 的输出后,再 add 之前,加了一个 0.1 的 dropout:
class AddNorm(nn.Module):
def __init__(self, normalized_shape, dropout, **kwargs):
super(AddNorm, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y): # x 为每个 sub-layer 的输出
return self.ln(self.dropout(Y) + X)
- 再 encoder 和 decoder 位置编码的输出后加入 dropout。(代码可以参考 positional encoding 部分)
Encoder Layer
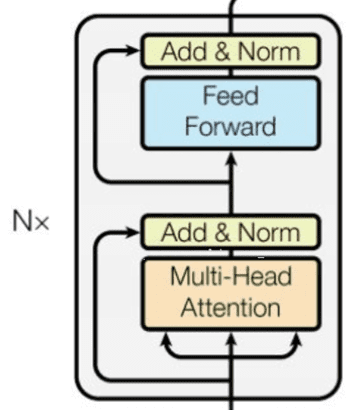
在拥有了全部的 encoder 组件之后,我们只需要根据上面这个图将 encoder block 给拼接起来就行了。于是就成了下面这个样子:
class EncoderBlock(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, use_bias=False, **kwargs):
super(EncoderBlock, self).__init__(**kwargs)
self.attention = d2l.MultiHeadAttention(key_size, query_size,
value_size, num_hiddens,
num_heads, dropout, use_bias)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
num_hiddens)
self.addnorm2 = AddNorm(norm_shape, dropout)
def forward(self, X, valid_lens):
Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
return self.addnorm2(Y, self.ffn(Y)) # [batch_size, len_seq, d_model]
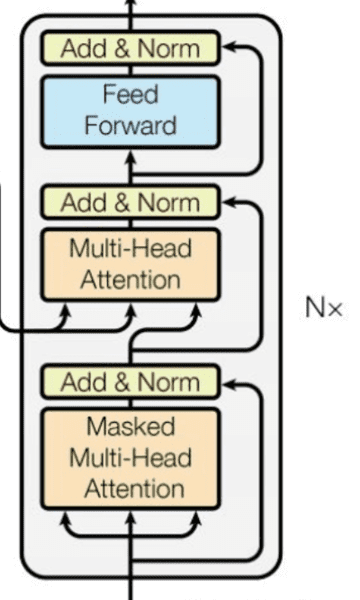
Decoder Layer
decoder layer 的组件和 encoder layer 很像,不同的一点是第二个 multi-head attention,里面使用对注意力机制使用了掩码,使得一个单词只能注意到前面的单词。并且他不是 self-attention,他的 key 和 Value 都来自 encoder 的输出。
class DecoderBlock(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, i, **kwargs):
super(DecoderBlock, self).__init__(**kwargs)
self.i = i
self.attention1 = d2l.MultiHeadAttention(key_size, query_size,
value_size, num_hiddens,
num_heads, dropout)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.attention2 = d2l.MultiHeadAttention(key_size, query_size,
value_size, num_hiddens,
num_heads, dropout)
self.addnorm2 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
num_hiddens)
self.addnorm3 = AddNorm(norm_shape, dropout)
def forward(self, X, state):
enc_outputs, enc_valid_lens = state[0], state[1]
# During training, all the tokens of any output sequence are processed
# at the same time, so `state[2][self.i]` is `None` as initialized.
# When decoding any output sequence token by token during prediction,
# `state[2][self.i]` contains representations of the decoded output at
# the `i`-th block up to the current time step
if state[2][self.i] is None:
key_values = X
else:
key_values = torch.cat((state[2][self.i], X), axis=1)
state[2][self.i] = key_values
if self.training:
batch_size, num_steps, _ = X.shape
# Shape of `dec_valid_lens`: (`batch_size`, `num_steps`), where
# every row is [1, 2, ..., `num_steps`]
dec_valid_lens = torch.arange(1, num_steps + 1,
device=X.device).repeat(
batch_size, 1)
else:
dec_valid_lens = None # 非训练的时候,input 都是一个一个放进来的,不需要掩码。
X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
Y = self.addnorm1(X, X2)
# Y (`batch_size`, `num_steps`, `num_hiddens`)
Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
# 第二层用的 K 和 V 都是 encoder 的 output。
Z = self.addnorm2(Y, Y2)
return self.addnorm3(Z, self.ffn(Z)), state
Encoder
将我们的 embedding 和位置编码组合,之后注入到由 6 个 encoder block 拼接而成的串中,就形成了 transformer 的 encoder:
class TransformerEncoder(d2l.Encoder):
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, use_bias=False, **kwargs):
super(TransformerEncoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module(
"block" + str(i),
EncoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, use_bias))
def forward(self, X, valid_lens, *args):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self.attention_weights = [None] * len(self.blks)
for i, blk in enumerate(self.blks):
X = blk(X, valid_lens)
self.attention_weights[
i] = blk.attention.attention.attention_weights
return X
Decoder
decoder 也是类似,对于每一个 decoder block 的第二个 multi-head attention,都需要用到 encoder 最后的输出。
class TransformerDecoder(d2l.AttentionDecoder):
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, **kwargs):
super(TransformerDecoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.num_layers = num_layers
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module(
"block" + str(i),
DecoderBlock(key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, dropout, i))
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
return [enc_outputs, enc_valid_lens, [None] * self.num_layers]
def forward(self, X, state):
# state[0]:编码层输出
# state[1]: 编码层输出对应的掩码
# state[2]:上一个 decoder block 的输入
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self._attention_weights = [[None] * len(self.blks) for _ in range(2)]
for i, blk in enumerate(self.blks):
X, state = blk(X, state)
# Decoder self-attention weights
self._attention_weights[0][
i] = blk.attention1.attention.attention_weights
# Encoder-decoder attention weights
self._attention_weights[1][
i] = blk.attention2.attention.attention_weights
return self.dense(X), state
@property
def attention_weights(self):
return self._attention_weights
Optimizer
学习率使用了一下的规划方案:
优化器使用的是 Adam optimizer,其中 , \beta _2 = 0.98, . 预热长度设置为了 warmup_steps = 4000。
训练和测试
训练时的步骤大致为:
- 原句子放入 encoder,输出了 encoder outputs。
- 将目标语句右移 1 位,并在开头加上句子开头编码
<BOS>。整个调整后的目标语句将会被放入 decoder 中同时进行训练。 - 在 decoder 的输出后加上一个线性层和一个 softmax。计算 cross entropy loss 然后进行梯度下降。
测试时候 decoder 比较不同:
- 测试时,decoder 一开始使用
<BOS>作为输入,这个和很多的机械翻译任务一样。 - 一个单词输入,通过 decoder 会得到一个单词输出。多次执行 decoder 直到
<EOS>。我们就可以得到一个句子了。 - 测试时候我们不需要对 decoder 的注意力层进行注意力掩码。
具体的可以参考 tensorflow 中的 transformer 机械翻译教程,温馨提示:那个教程当中 multi-head attention 的做法和原本论文的表达不是很一致,而且也存在很大的局限性。如果你没觉得有啥不同,那可能是我记错了。