GCN 的提出打开了网络算法的新世界，但仍有部分局限性。传统注意力机制包括 Attention for image Captioning 和 for Machine Translation。但是传统的注意力目前较少人使用。近期的 seq2seq, transformers 使用的自注意力越来越多人使用。GAT 加入自注意力机制，大大提高了各方面的效果，但其计算资源消耗也大幅度的提高了。在实际应用中，基本上当 GCN 准确率在 70%、80%遇到瓶颈的时候，如果硬件有条件，可以考虑使用 GAT。

GAT

为什么使用 GAT

一部分模型依赖于拉普拉斯算子进行学习，如 GCN。而拉普拉斯算子取决于图结构，因此当这一类模型在一个图结构上训练后，不能够直接应用到新的、不同的图结构上。

GCN 节点权重是固定的。

GCN 设计时候考虑的是无向图。当我们在有向图上处理 GCN 时（如 Cora），需要将原始邻接矩阵转变为对称的邻接矩阵来作为 GCN 的输入。即： adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

针对上面三个问题，GAT 都进行了优化。

GAT 架构

GAT 的输入为节点的特征，其中 $F$ 为特征维度，$N$ 为节点个数：

$$\mathbf{h}=\left\{\vec{h}_{1}, \vec{h}_{2}, \ldots, \vec{h}_{N}\right\}, \vec{h}_{i} \in \mathbb{R}^{F}$$

我们使用一个共享的线性变换矩阵 $\mathbf{W} \in \mathbb{R}^{F^{\prime} \times F}$​ 与一个共享的注意力机制 $a$ 来计算节点之间的边系数计算方式为：

$$e_{i j}=a\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)\tag1$$

(当然的节点的相似度，也可以通过点，边或者 motif 来衡量。或者使用图论中点的相似度计算方式。)

之后在进行 softmax 对注意力系数归一化得到两点之间的注意力权重 $\alpha_{ij}$​：

$$\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}\tag2$$

公式 $(1),(2)$ 综合为：

$$\alpha_{i j}=\frac{\exp \left(\text { LeakyReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\text { LeakyReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)}$$

其中，注意力机制 $a$ 为一个单层的前向神经网络，权重为 $\overrightarrow{\mathbf{a}} \in \mathbb{R}^{2 F^{\prime}}$ ，激活函数使用了$\alpha=0.2$​ 的 LeakyReLU。​

最后将邻居节点投影后根据注意力权重加权求和，经过一个非线性变换 $\sigma$​ （论文实验环节的配置为 ELU），得到新的 i 节点特征 $\vec{h}_{i}^{\prime}$​。​

$$\vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)$$

相关图片

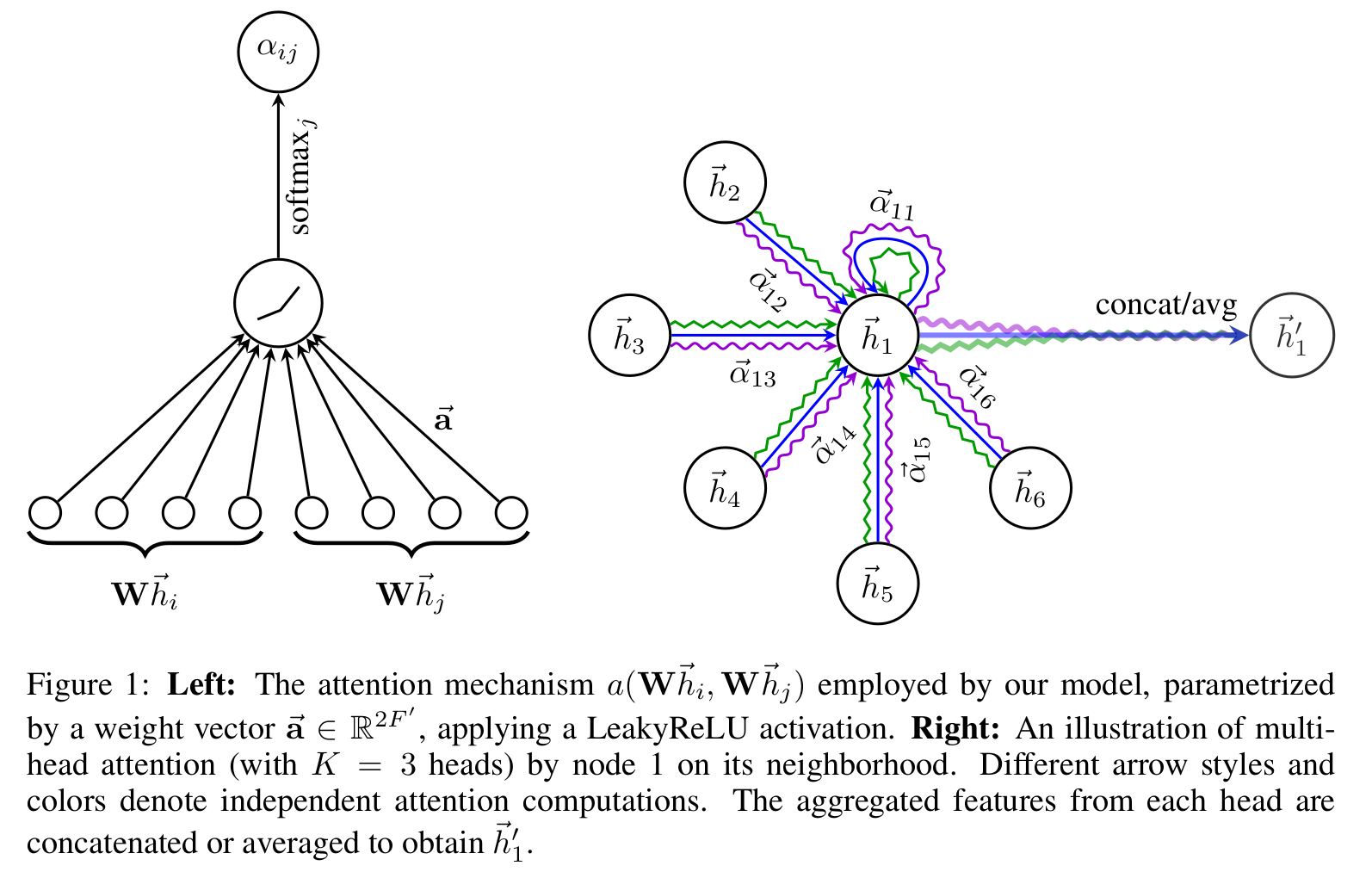
当使用多头注意力的时候，与 transformer 类似的，我们将邻居节点进行 k 次不同的注意力机制，如下：

$$\vec{h}_{i}^{\prime}=\|_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)$$

其中 $W^k$​ , $\alpha^k_{ij}$​​​​ ​为每个头对应的参数。中间层的多头注意力计算可以使用拼接的方式求得，但在最后一个输出层则需要对所有注意力头的结果取平均。

$$\vec{h}_{i}^{\prime}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)$$

整个算法的时间复杂度为 $O\left(|V| F F^{\prime}+|E| F^{\prime}\right)$​ 由于算法设计了大量系数矩阵的计算，GPU 可能不能带来非常大的性能提升。

测试与结果

image-20210823155431970

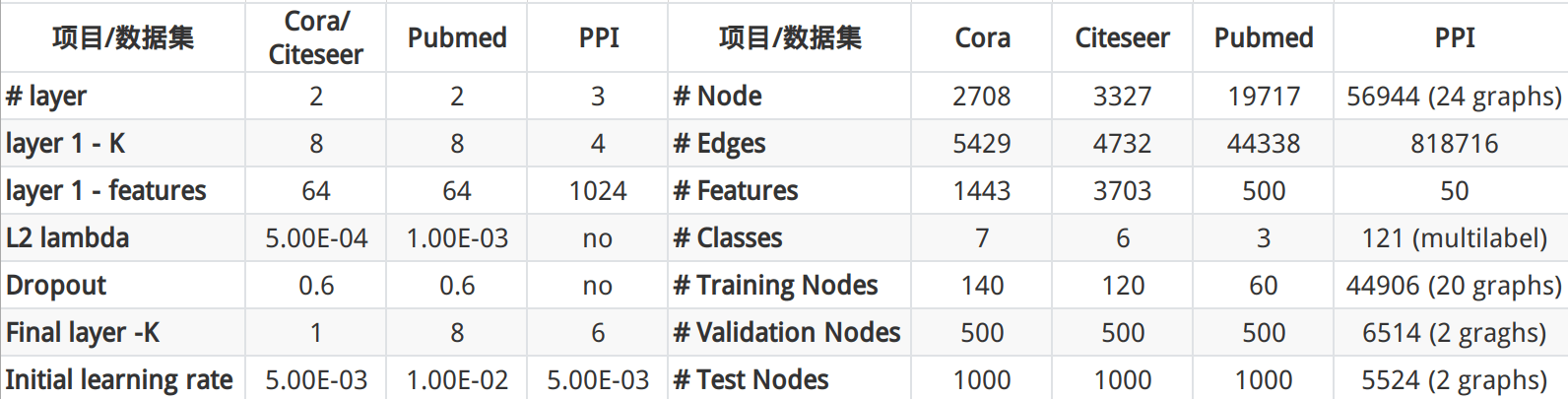
论文作者考虑到 Pubmed 训练集只有 60 个样本，因此将输出层的注意力头数量 K 从 1 改为了 8，并且提高了 L2 的惩罚系数。

在 PPI 数据集训练中，作者还给网络加上了残差链接。

从实验结果可以看出，GAT 在 Transductive 任务上比同规模的 GCN 高 1 个百分点左右。而在 Inductive 任务中，效果更是比 GraphSAGE 好了 0.2+。

相关图片

相关图片

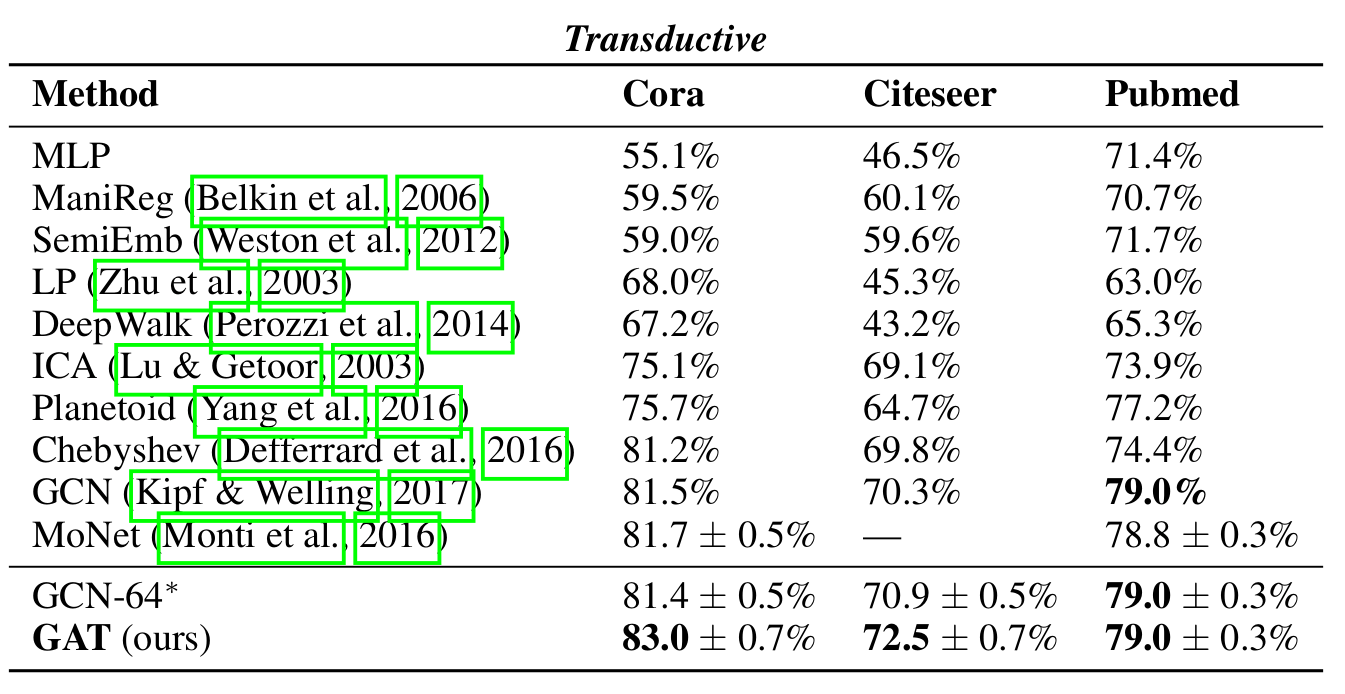
根据论文的时间结果看来，对于 Transdutive 任务，从硬件条件和计算成本来看，我们还是可以考虑使用效果稍微差那么一点的 GCN。而在 Inductive 任务上，若简单的 GraghSAGE 并不能满足任务需求的话，采用 GAT 会是一个不错的优化方向。

可视化

image-20210822162530925

这是在 Cora 数据集上的 t-SNE 可视化结果，点之间的连线深度表示了点之间的注意力权重。

相关代码

佛系更新...

参考

1. 论文链接 Graph Attention Networks