图卷积神经网络 GCN
不同的数据结构使得学者们创造了不同的特征提取和编码方式,例如 CNN 的卷积核很好地应用在了图像编码上,RNN 的结构更好地提取了文本或者其他序列数据的时间步信息。GCN 的设计是为了对图谱,社交网络等图结构数据有更好的解析能力。
GCN 可以做 节点分类(node classification)、图分类(graph classification)、边预测(link prediction) ,同时也可以提取 图相关的嵌入(graph embedding)
简单讲讲图
图论历史 - 三次里程碑
1735 年 8 月 26 日,欧拉向当时俄国的圣彼得堡科学院递交了一篇名为《有关位置几何的一个问题的解》的论文,阐述了他是如何否定哥尼斯堡七桥问题能一次走完的。而后人们认识到可以用点与线来描述具体问题,以此引发了对图论的继续研究。引用-从七桥问题开始说图论
在 1959 和 1968 年期间,数学家 Paul Erdos 和 Alfred Renyi 发表了关于随机图( Random Graph )的一系列论文,在图论的研究中融入了组合数学和概率论,建立了一个全新的数学领域分支---随机图论。引用-随机图模型
1999 年 Barabasi 提出了 Scalefree network 无标度网络。引用-什么是无标度网络 | 集智百科,无标度网络模型开山之作:随机网络中标度的涌现
图基础
图根据是否有向 directed 与是否有权重 weighted 可以分成四类图。现实中的数据,大部分都是有权重的,无权重的图论主要在理论界发展。
度分布
节点度通常定义为该节点所有连接边的数量,网络的度分布即为网络中各节点的度的概率分布或者频率分布。
对于随机图,度分布为
其中 为 一个定点恰好度数为 的概率,当 时,度分布近似与泊松分布。
其中点平均度数
对于无标度网络,度分布呈幂率分布
通常 在 2 到 3 之间。
距离衡量 Distance
GCN 对距离的要求:1. 点与点之间的权重为正。2. 节点之间的距离计算,需要在线性时间复杂度内。
希尔伯特空间为完备空间,他的内积运算满足:
(1) (2) (3) (4) 若 , 则
其中 a 为复数域上的一个数, 为线性空间中的任意三个矢量。
聚类系数 Clustering Coefficient
聚类系数 Clustering coefficient 可用于衡量网络的稠密程度。
局部聚类系数(面向节点)
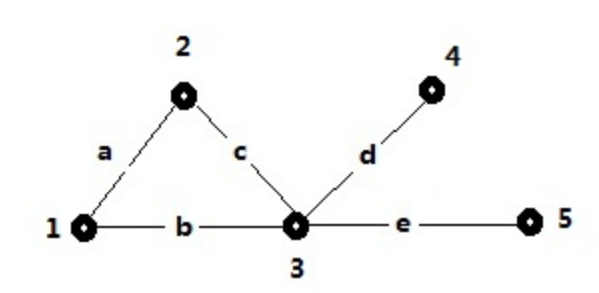
例如,对于节点 3,他的 closed triplet (triangles) 为 {3,(1,2)},所有的 triplet 为 {3,(1,2)},{3,(2,4)},{3,(4,5)},{3,(1,5)},{3,(2,5)},{3,(1,4)},因此他的 3 节点的局部聚类系数为:1/6。
全局聚类系数则面向所有的节点
(计算 triple 时候,i 需要作为中间(枢纽)节点)
聚类系数(clustering coefficient)计算
中介度 Betweeness
点界度 node Betweeness:
节点 i 的点界度计算方式为: 其中 L 为最短路径
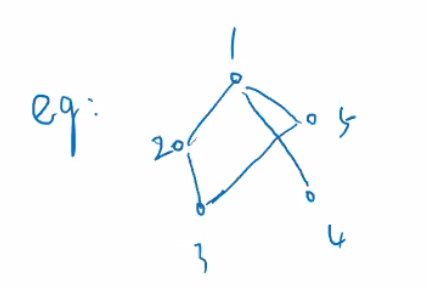 以点 1 点界度计算为例:
以点 1 点界度计算为例:
计算点 1 的点界度时,依次计算所有两点组合的最短路径数量,以及最短路径中有经过点 1 的路径数量。
边界度 edge betweeness
边界度与点界度的计算方式相似,边 的计算方法为:
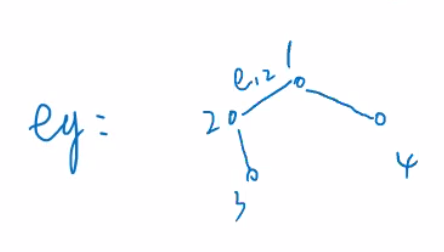 以 的计算为例:
以 的计算为例:
betweeness 用来衡量节点或者边的流通性,对于搜索桥接点十分有帮助。
其他基本概念
walk,trail, path , tree ,complementary gragh,perfect match,bridge,Eulerian Gragh,Hamiltonian graph, Motif / subgragh , coreness ,hyper gragh (HGCN)
拉普拉斯算子

对于基函数 ,其拉普拉斯算子为:
即 为自身拉普拉斯算子的特征向量。
图上节点拉普拉斯算子定义
首先定义 节点特征向量 ,
而后定义节点 的拉普拉斯算子为: 节点与邻上节点的差值总和。推导
所以
图上傅里叶变化的定义
因为拉普拉斯算子的特征向量为 ,对拉普拉斯算子进行 SVD 特征展开后,得到 ,因此图的傅里叶变化为。此处并没有严格的数学推导,存在部分的近似代替与逻辑推理。
GCN
考虑一个图结构的数据,其中有 N 个节点, 为节点的特征矩阵,节点之间的邻接矩阵(adjacency matrix)为 。
GCN 目的是建立一个模型 ,使得给定输入 ,输出 , 其中 为我们所需要的每个节点的特征数量。
首先考虑这个简单的模型结构:
其中 是每一层的 activation,\text{ 是激活函数 },\text{ 如 }
以上模型有两个缺点:
- 特征矩阵与对角线全为 0 的邻接矩阵 点积,这意味着每个节点都可以考虑到其他节点的信息,缺遗漏了节点本身的信息。解决方式就是给他加上一个单位矩阵 。
- A 一般都是没有归一化的,所以特征矩阵与 A 点积将使得节点特征的规模(scale) 产生变化。可以使用 random walk normalization ,其中 是度矩阵 (degree matrix)。然而 GCN 使用的是 symmetric normalization 。symmetric normalization 同时考虑了 edge 上两端节点的度。
在改进后,GCN 有了以下层与层之间的结构:
其中
l 论文中以下面这个双层网络结构解释了 GCN 的优化过程:
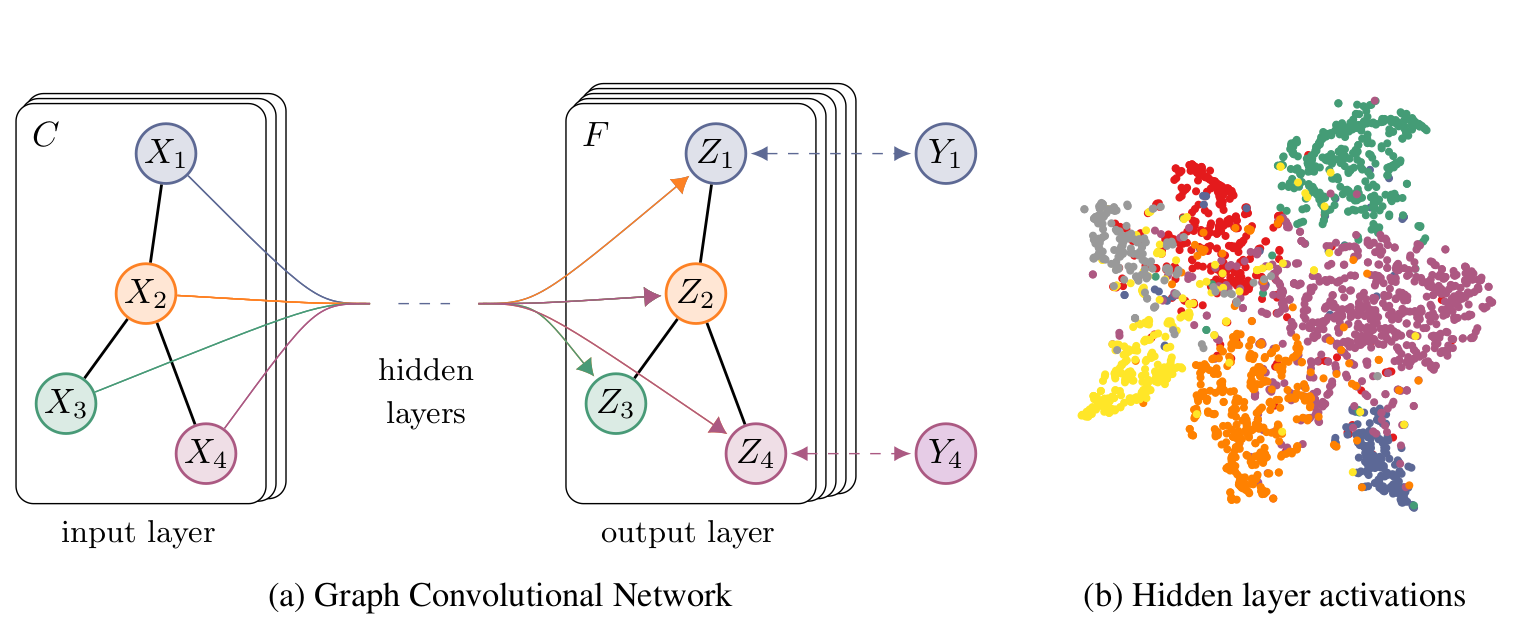
左图为我们的网络结构,右图在 Cora 数据集上训练后的 activation 可视化(t-SNE)
由于数据集中只有小部分有标注,因此我们只对有标注的序列计算交叉熵。
图卷积的演变
第一代的 GCN 卷积核为
其中 x 为特征矩阵。因为没有归一化,存在收敛问题。同时也没有考虑点对自身的影响。计算复杂度也在 。
第二代的卷积核解决了自身权重与归一化的问题。二代使用了切比雪夫展开,
而后第三代卷积核加入了切比雪夫展开的前两项的近似优化,并对其中某些参数进行了定义,解决了时间复杂度问题,最终形成了目前使用的公式。
代码实例
官方 torch 代码 repo
数据处理
cora 数据集有 cora.content 与 cora.cities 两个文件。其中 content 文件格式为 paper_id x_1 x_2 ... x_i y x 为 1433 维向量的 0/1 整数,代表词表中对应编码的词是否出现在该文中,y 为论文的类别。cities 文件格式为 paper_id1 paper_id2 表示 这两个论文之间存在引用关系。
邻接矩阵
邻接矩阵的维度为 (论文数,论文数) ,若论文 i 引用了 j ,则A[i,j]=1 。实际代码中采用了稀疏矩阵进行储存,并且需要将临街矩阵的 idx 与特征矩阵对应。
idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
idx_map = {j: i for i, j in enumerate(idx)}
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),dtype=np.int32)
edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
dtype=np.int32).reshape(edges_unordered.shape)
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
shape=(labels.shape[0], labels.shape[0]),
dtype=np.float32)
得到邻接矩阵 后, 将有向图转变为无向图,保留权重最大的边 。而后再处理成 :
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
adj = normalize(adj + sp.eye(adj.shape[0]))
这边的归一化可以简单的按行处理,也可以根据上面公式进行对称归一化 (symmetric normalization)。
特征矩阵
特征矩阵的处理十分朴素,唯一要注意的就是这边做了归一化。
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
features = normalize(features)
标签 Label
labels = encode_onehot(idx_features_labels[:, -1])
labels = torch.LongTensor(np.where(labels)[1])
辅助函数
def normalize(mx):
rowsum = np.array(mx.sum(1))
r_inv = np.power(rowsum, -1).flatten()
r_inv[np.isinf(r_inv)] = 0.
r_mat_inv = sp.diags(r_inv)
mx = r_mat_inv.dot(mx)
return mx
模型结构
模型中比较特别的是,采用了 sparse mm 的计算方法。
class GCN(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout):
super(GCN, self).__init__()
self.gc1 = GraphConvolution(nfeat, nhid)
self.gc2 = GraphConvolution(nhid, nclass)
self.dropout = dropout
def forward(self, x, adj):
x = F.relu(self.gc1(x, adj))
x = F.dropout(x, self.dropout, training=self.training)
x = self.gc2(x, adj)
return F.log_softmax(x, dim=1)
class GraphConvolution(Module):
"""
Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
"""
def __init__(self, in_features, out_features, bias=True):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.FloatTensor(in_features, out_features))
if bias:
self.bias = Parameter(torch.FloatTensor(out_features))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)
def forward(self, input, adj):
support = torch.mm(input, self.weight)
# Sparse matrix multiplication,https://github.com/tkipf/pygcn/issues/19
# output = torch.spmm(adj, support)
output = torch.sparse.mm(adj, support)
if self.bias is not None:
return output + self.bias
else:
return output
def __repr__(self):
return self.__class__.__name__ + ' (' \
+ str(self.in_features) + ' -> ' \
+ str(self.out_features) + ')'
训练细节
为了保持邻接矩阵的完整,在训练中我们使用 idx 的方式来分割训练,验证和测试集。
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
更新梯度或者计算指标时:
output = model(features, adj)
loss_train = F.nll_loss(output[idx_train], labels[idx_train])
acc_train = accuracy(output[idx_train], labels[idx_train])