谈谈这些 GCN 模型 - NRI、RGCN

读论文总是枯燥且难熬呢，于是便尝试在阅读时便对论文进行了知识点的梳理与记录，希望有助于加深理解与记忆。希望这份笔记也能提供一些小小的帮助

本文总结的模型为 NRI（Neural Relational Inference for Interacting Systems）、RGCN（Modeling Relational Data with Graph Convolutional Networks）。

NRI

NRI 出自论文：Neural Relational Inference for Interacting Systems。在有向图与无向图都可以使用。

背景

相关图片

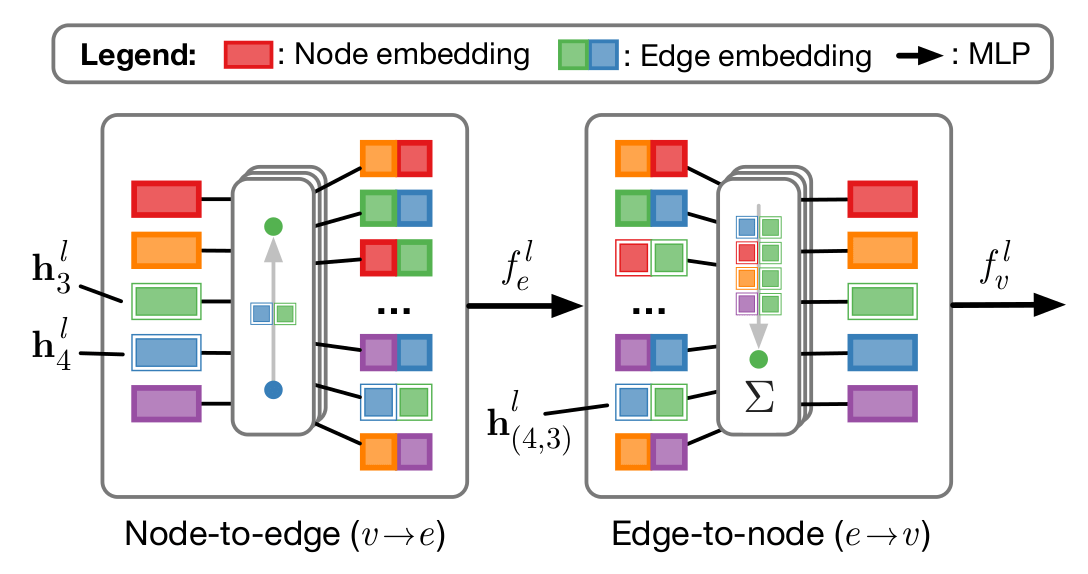
（图：GNN 点之间的前向传播）

首先讨论一下 GNN，传统的 GNN 可以定义为以下节点到节点的传播

$$\begin{aligned} v \rightarrow e: & \mathbf{h}_{(i, j)}^{l}=f_{e}^{l}\left(\left[\mathbf{h}_{i}^{l}, \mathbf{h}_{j}^{l}, \mathbf{x}_{(i, j)}\right]\right) \\ e \rightarrow v: & \mathbf{h}_{j}^{l+1}=f_{v}^{l}\left(\left[\sum_{i \in \mathcal{N}_{j}} \mathbf{h}_{(i, j)}^{l}, \mathbf{x}_{j}\right]\right) \end{aligned}$$

其中 [·，·] 为拼接操作，$x_i,x_{i,j}$​ 分别表示节点 $i$ 与节点 $i,j$ 的特征表示。而 $h$​ 表示在传递过程中发生了改变的节点特征。

NRI 架构

image-20210825141413551

首先定义：

• 节点在时间步 $t$ 的特征向量为：$\mathbf{x}^{t}=\left\{\mathbf{x}_{1}^{t}, \ldots, \mathbf{x}_{N}^{t}\right\}$​
• 节点 i 的特征向量由 T 个时间步组成：$\mathbf{x}_{i}=\left(\mathbf{x}_{i}^{1}, \ldots, \mathbf{x}_{i}^{T}\right)$​
• $z$​ 边类型 (discrete edge type)， $z_{ij}$​​ 为点 $i,j$​ 之间的边属性。

对于 $z$​，可以将他理解为 LDA 中的隐藏主题。即代表了连个节点之间的复杂关系，如节点 $i,j$​ 代表了 A,B 两个人，他们之间的隐藏关系可能是情侣，同桌，舍友。此时隐变量 $z=[0.1,0.4,0.5]$​​​ 便可以代表对应关系的概率。

优化目标

NRI 采用了 VAE，优化对象为 ELBO：

$$\mathcal{L}=\mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log p_{\theta}(\mathbf{x} \mid \mathbf{z})\right]-\mathrm{KL}\left[q_{\phi}(\mathbf{z} \mid \mathbf{x}) \| p_{\theta}(\mathbf{z})\right]$$

Encoder

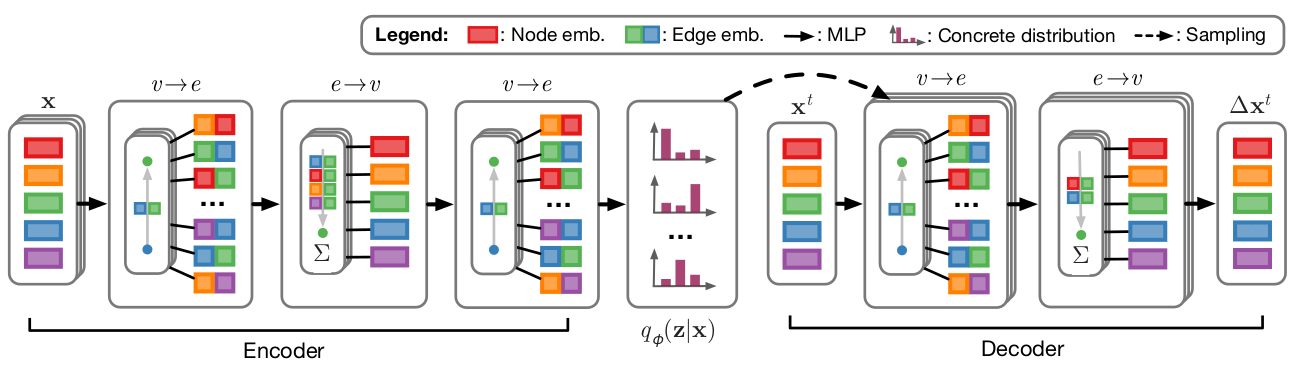
(图：NRI 框架图)

NRI 的 encoder 操作与 GNN 类似，不过它由三层 MLP 构成，大致思想是：首先通过 1，2 步进行节点信息的更新。而后使用更新后的节点信息输出边信息求隐变量 z。

$$\begin{aligned} \mathbf{h}_{j}^{1} &=f_{\mathrm{emb}}\left(\mathbf{x}_{j}\right) \\ v \rightarrow e: \quad \mathbf{h}_{(i, j)}^{1} &=f_{e}^{1}\left(\left[\mathbf{h}_{i}^{1}, \mathbf{h}_{j}^{1}\right]\right) \\ e \rightarrow v: \quad \mathbf{h}_{j}^{2} &=f_{v}^{1}\left(\sum_{i \neq j} \mathbf{h}_{(i, j)}^{1}\right) \\ v \rightarrow e: \quad \mathbf{h}_{(i, j)}^{2} &=f_{e}^{2}\left(\left[\mathbf{h}_{i}^{2}, \mathbf{h}_{j}^{2}\right]\right) \end{aligned}$$

经过以上编码器后可以求得 edge type posterior：

$$q_\phi(z_{ij}|x) = softmax(h^2_{(i,j)})$$

Sampling

由于上一步得到的 $q_\phi(z_{ij}|x)$ 服从离散分布，因此作者从下面这个近似的连续分布中进行了采样：

$$\mathbf{z}_{i j}=\operatorname{softmax}\left(\left(\mathbf{h}_{(i, j)}^{2}+\mathbf{g}\right) / \tau\right)$$

其中，$\mathbf{g} \in \mathbb{R}^{K}$​​​ 是从 Gumbel(0,1) 分布中采集的随机值。$\tau$​ 为 softmax 的 temperature。

Decoder

$$\begin{aligned} v \rightarrow e: \quad \tilde{\mathbf{h}}_{(i, j)}^{t} &=\sum_{k} z_{i j, k} \tilde{f}_{e}^{k}\left(\left[\mathbf{x}_{i}^{t}, \mathbf{x}_{j}^{t}\right]\right) \\ e \rightarrow v: \quad \boldsymbol{\mu}_{j}^{t+1} &=\mathbf{x}_{j}^{t}+\tilde{f}_{v}\left(\sum_{i \neq j} \tilde{\mathbf{h}}_{(i, j)}^{t}\right) \\ p\left(\mathbf{x}_{j}^{t+1} \mid \mathbf{x}^{t}, \mathbf{z}\right) &=\mathcal{N}\left(\boldsymbol{\mu}_{j}^{t+1}, \sigma^{2} \mathbf{I}\right) \end{aligned}$$

其中 $z_{ij,k}$ 表示向量 $z_{ij}$ 的第 k 个元素，$\sigma^2$ 为一个固定方差。

论文中使用了两个方法来解决塌陷问题：

• 预测未来多个时间步的值
• 对每个 edge type 采用独立的 MLP。

预测未来多个时间步的值 这一步中，作者将解码层的输入$x^t$ 更换为 $\mu^t$ 。如果我们将上述 Decoder 的传播定义为 $\boldsymbol{\mu}_{j}^{t+1}=f_{\mathrm{dec}}\left(\mathbf{x}_{j}^{t}\right)$​​ ，则计算流程将改变为：

$$\begin{array}{rlr} \boldsymbol{\mu}_{j}^{2} & =f_{\mathrm{dec}}\left(\mathbf{x}_{j}^{1}\right) & \\ \boldsymbol{\mu}_{j}^{t+1} & =f_{\mathrm{dec}}\left(\boldsymbol{\mu}_{j}^{t}\right) & \quad t=2, \ldots, M \\ \boldsymbol{\mu}_{j}^{M+2} & =f_{\operatorname{dec}}\left(\mathbf{x}_{j}^{M+1}\right) & \\ \boldsymbol{\mu}_{j}^{t+1} & =f_{\mathrm{dec}}\left(\boldsymbol{\mu}_{j}^{t}\right) & t=M+2, \ldots, 2 M \end{array}$$

GRU 解码

考虑到原来 decoder 遵循的马尔科夫假设在大多数情况下不成立。作者采用了 RNN 结构进行解码，使用的单元为 GRU。具体操作如下：

$$\begin{aligned} v \rightarrow e: \quad \tilde{\mathbf{h}}_{(i, j)}^{t} &=\sum_{k} z_{i j, k} \tilde{f}_{e}^{k}\left(\left[\tilde{\mathbf{h}}_{i}^{t}, \tilde{\mathbf{h}}_{j}^{t}\right]\right) \\ e \rightarrow v: \quad \mathrm{MSG}_{j}^{t} &=\sum_{i \neq j} \tilde{\mathbf{h}}_{(i, j)}^{t} \\ \tilde{\mathbf{h}}_{j}^{t+1} &=\operatorname{GRU}\left(\left[\mathrm{MSG}_{j}^{t}, \mathbf{x}_{j}^{t}\right], \tilde{\mathbf{h}}_{j}^{t}\right) \\ \boldsymbol{\mu}_{j}^{t+1} &=\mathbf{x}_{j}^{t}+f_{\text {out }}\left(\tilde{\mathbf{h}}_{j}^{t+1}\right) \\ p\left(\mathbf{x}^{t+1} \mid \mathbf{x}^{t}, \mathbf{z}\right) &=\mathcal{N}\left(\boldsymbol{\mu}^{t+1}, \sigma^{2} \mathbf{I}\right) \end{aligned}$$

实验与结果

实验采用了物理仿真数据集，这些实验系统有着简单的规律，但却能够表现出复杂的动态形式。因此模型会尝试从复杂的动态中发现隐藏的规则，如下图所示，模型对轨迹的预测效果很好。

image-20210825155803345

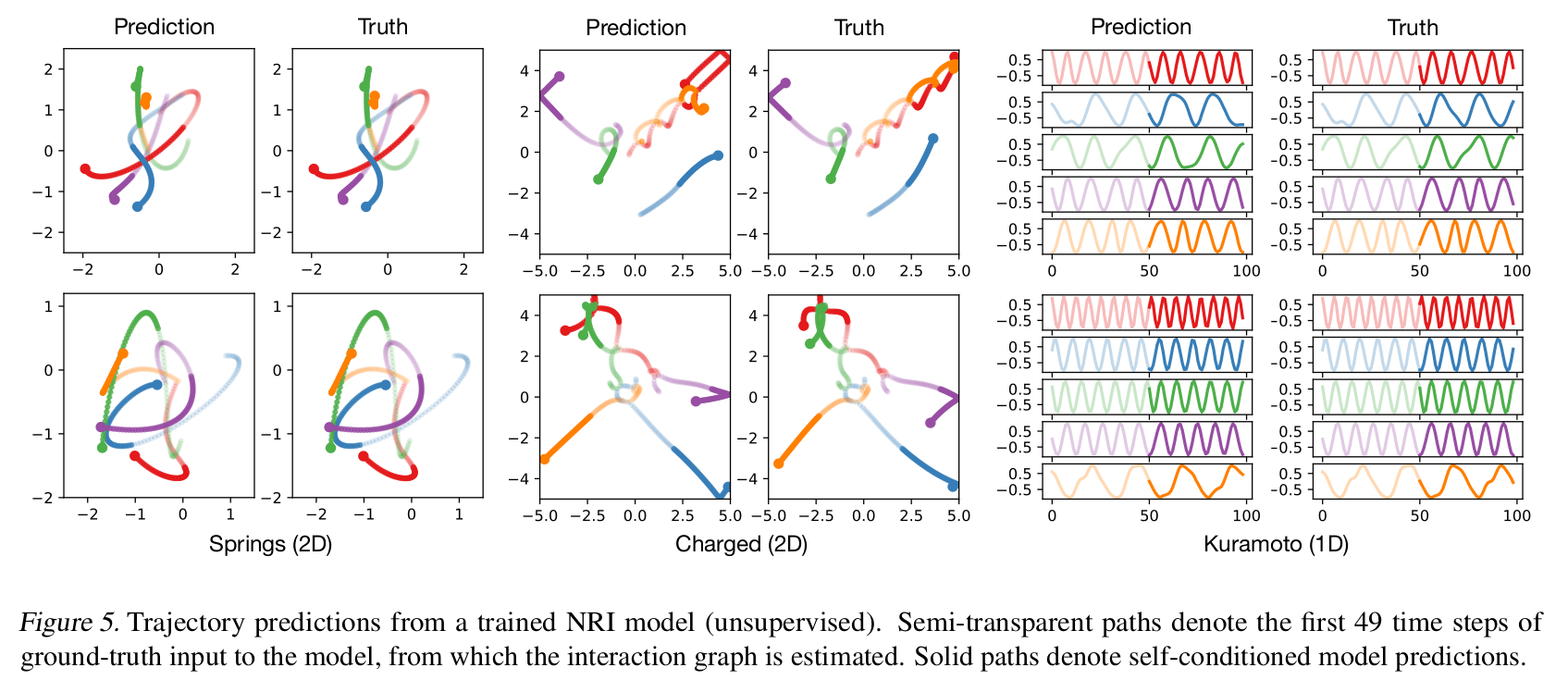
监督学习下的三个实验也都达到了 94+%的准确率。尽管数据集不是真实的，但符合物理与数学逻辑，感觉实验结果还是具有部分参考价值的。

RGCN

RGCN 出自 Modeling Relational Data with Graph Convolutional Networks ，最近在知识图谱领域用的比较多。RGCN 采用了 GCN 的思想，并将其应用在了知识图谱上，论文对 Link Predition 和 entity classification 连个任务进行了研究。

模型架构

首先，定义有向的、多重的、有标记的图（directed and labeled multi-graphs） 为$G=(\mathcal{V}, \mathcal{E}, \mathcal{R})$​​，其中 $v_{i} \in \mathcal{V}$ 为节点，有标记的边为 $\left(v_{i}, r, v_{j}\right) \in \mathcal{E}$, 节点之间的关系类型为 $r \in \mathcal{R}$​ 。受到 GCN 的启发，论文作者在 relational (directed and labeled) multi-graph 上定义了以下前向传导方式：

$$h_{i}^{(l+1)}=\sigma\left(\sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}_{i}^{r}} \frac{1}{c_{i, r}} W_{r}^{(l)} h_{j}^{(l)}+W_{0}^{(l)} h_{i}^{(l)}\right)$$

其中 $c_{i,r}$​ 为归一化因子。$h^{(l)}_i\in\mathbb R^{d^{(l)}}$

相关图片

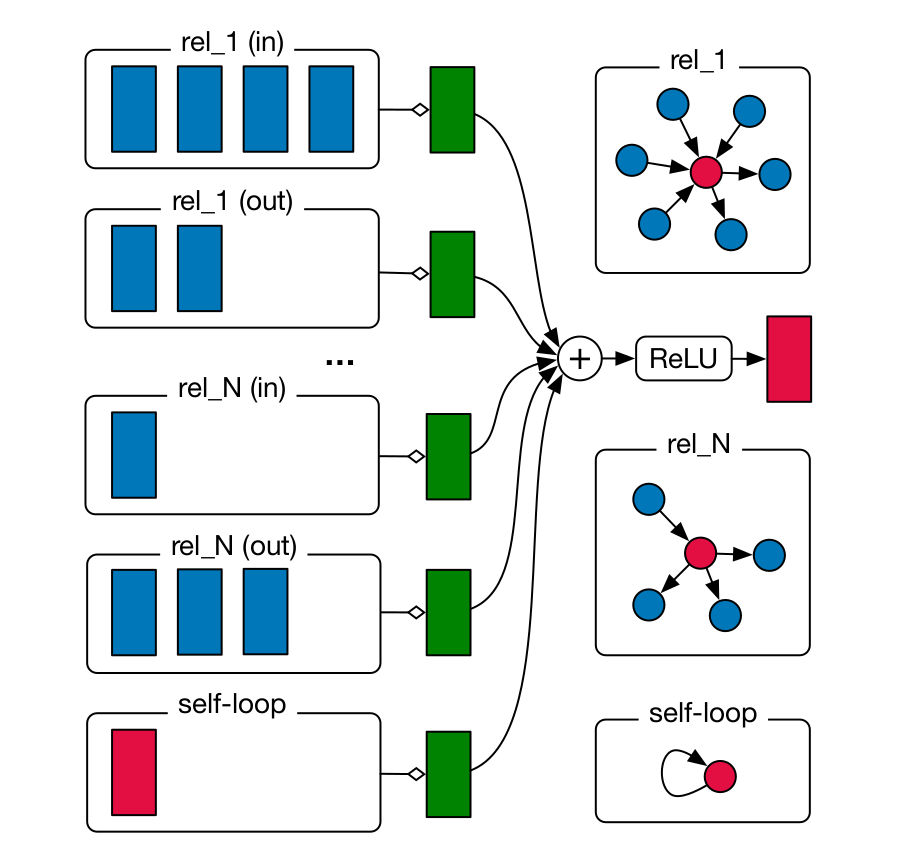
（图：R-GCN 在有向图上的前向传导）

Regularization

通过 decomposition，减小训练参数，提高训练效率，同时起到了防止过拟合的效果。R-GCN 采用了一下两种分解方式：

基础分解 basis decomposition

这种方式可以考虑成不同点间关系的权重共享。

$$W_{r}^{(l)}=\sum_{b=1}^{B} a_{r b}^{(l)} V_{b}^{(l)}$$

其中 $V_b^{(l)}\in \mathbb{R}^{d^{(l+1)}\times d^{(l)}}$​ ，超参 $B$ 用来调整分解的力度。通过矩阵分解，从 $l$ 层到 $l+1$ 层上的 $W^{(l)}$ 参数数量从 $r\times d^{(l+1)}\times d^{(l)}$ 减少到了 $(d^{(l+1)}\times d^{(l)} + r)\times B$​​​​ 。根据论文末的节点分类讨论，B 的范围大概在 $\{0, 10, 20, 30, 40\}$, 0 表示不使用 decomposition。​

Block-diagonal decomposition

对 $W^{(l)}_r$ 进行 LDU 分解，保留矩阵 D。

$$W_{r}^{(l)}=\bigoplus_{b=1}^{B} Q_{b r}^{(l)}=\operatorname{diag}\left(Q_{1 r}^{(l)}, \ldots, Q_{B r}^{(l)}\right)$$

其中 $Q_{b r}^{(l)} \in \mathbb{R}^{\left(d^{(l+1)} / B\right) \times\left(d^{(l)} / B\right)}$

Entity classification

节点分类预测的操作与 GCN 类似，在输出层使用 softmax 激活函数。然后训练时候最小化交叉熵损失：

$$\mathcal{L}=-\sum_{i \in \mathcal{Y}} \sum_{k=1}^{K} t_{i k} \ln h_{i k}^{(L)}$$

其中 $\mathcal{Y}$​​ 表示带有标记的节点，$t_{ik}$​​ 为 ground truth。$h^{(L)}_i$​​ 为节点 $i$​​​ 在输出层的 hidden state。​

Link Prediction

在这个任务中，作者首先将节点信息 $v_i \in V$​​ 使用 R-GCN 进行编码，得到了 $e_i = h^{(L)}_i,e_i\in\mathbb R^d$​​。而后每两个节点和他们之间可能的关系可构成三元组 (subject, relation, object)，使用解码器对这些三元组进行打分，得到两点之间的关系预测。在实验中，作者使用了 DistMult factorization[1] 作为得分方程：

$$f(s, r, o)=e_{s}^{T} R_{r} e_{o}$$

其中 $R_r\in \mathbb R ^{d\times d}$ 。在训练中采用了负采样的训练方式，优化目标为：

$$\begin{array}{r} \mathcal{L}=-\frac{1}{(1+\omega)|\hat{\mathcal{E}}|} \sum_{(s, r, o, y) \in \mathcal{T}} y \log l(f(s, r, o))+ \\ (1-y) \log (1-l(f(s, r, o))) \end{array}$$

其中 $\mathcal{T}$​ 为所有三元组的集合，$l$​ 为 sigmoid 函数，$y$ 为 indicator，0 表示负样本，1 表示正样本。​

实验结果

Entity Classification

作者使用了关系型数据集 AIFB, MUTAG, BGS, 和 AM 对 Entity Classification 任务进行测试。

相关图片

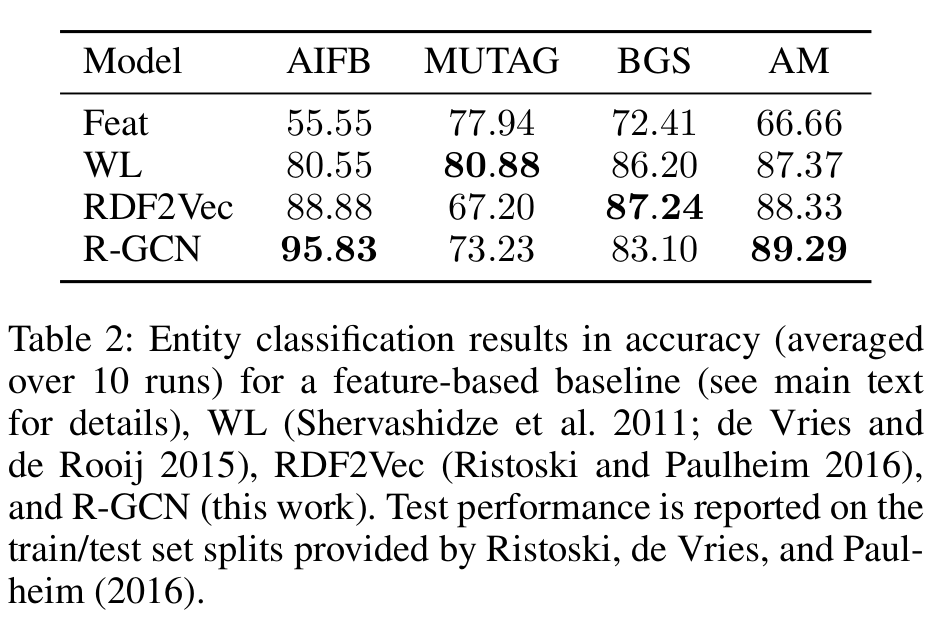
R-GCN 在 AIFB 和 AM 上都取得了 SOTA，对 MUTAG 和 BGS 的效果却没那么好。作者猜测，如果在权重计算时引入注意力机制，而非采用固定的归一化系数 $1/c_{i,j}$​​，效果应该会更好。

Link Prediction

该任务采用的数据集为 WN18，去除了 inverse triplet pairs 的 FB15K-237 和 FB15k。在训练过程中，作者对编码层采用了 edge dropout (对 self-loop 是 0.2，对其他节点是 0.4)，解码层采用了 0.01 的 l2 regularization。

image-20210826145322226

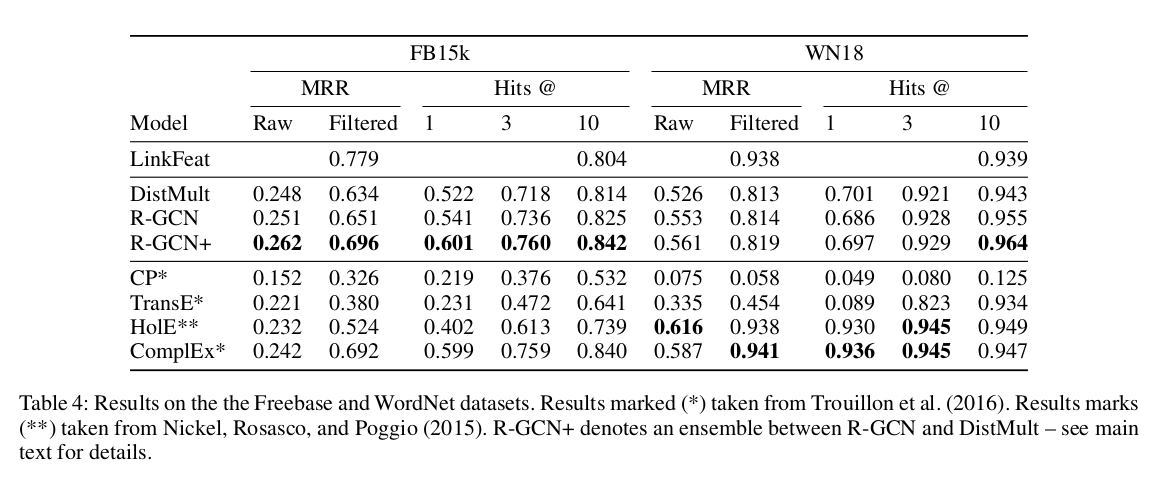
(图：FB15k, WN18 实验结果。)

其中 R-GCN+ 表示 DistMult 和 R-GCN 的 ensemble 模型。

$$\begin{array}{l} f(s, r, t)_{\mathrm{R}-\mathrm{GCN}+}= \alpha f(s, r, t)_{\mathrm{R}-\mathrm{GCN}}+(1-\alpha) f(s, r, t)_{\text {DistMult }} \end{array}$$

相关图片

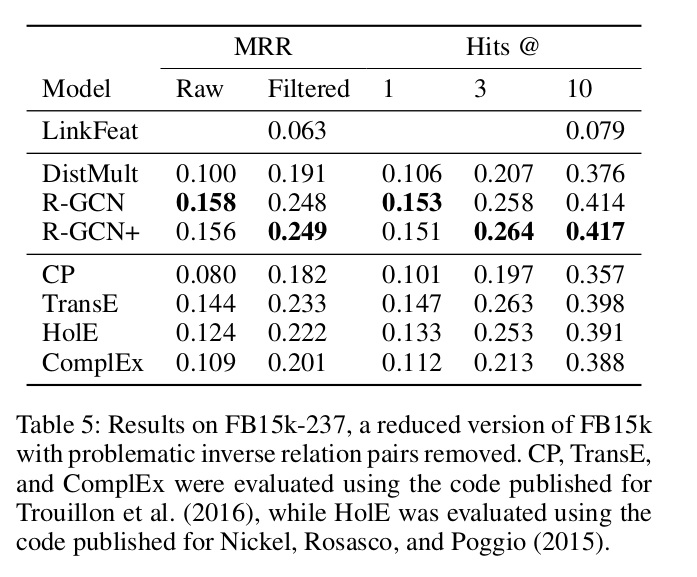
(图：FB15k-237 实验结果)

其他参考

1. Yang, B.; Yih, W.-t.; He, X.; Gao, J.; and Deng, L. 2014. Embedding entities and relations for learning and inference in knowledge bases. arXiv preprint arXiv:1412.6575.