纸上谈兵系列 - CompGCN、KGNN

读论文总是枯燥且难熬呢，于是便尝试在阅读时便对论文进行了知识点的梳理与记录，希望有助于加深理解与记忆。希望这份笔记也能提供一些小小的帮助

本文总结的模型为 CompGCN（Composition-Based Multi-Relational Graph Convolutional Networks）、KGNN （Knowledge-aware Graph Neural Networks with Label Smoothness Regularization for Recommender Systems）

CompGCN

CompGCN 来自 Composition-Based Multi-Relational Graph Convolutional Networks。它在节点更新方式上做了优化，减小了参数数量，大大降低了运算时间开销，效果也不错，但个人认为模型可解释性感觉差了那么一点。

模型架构

相关图片

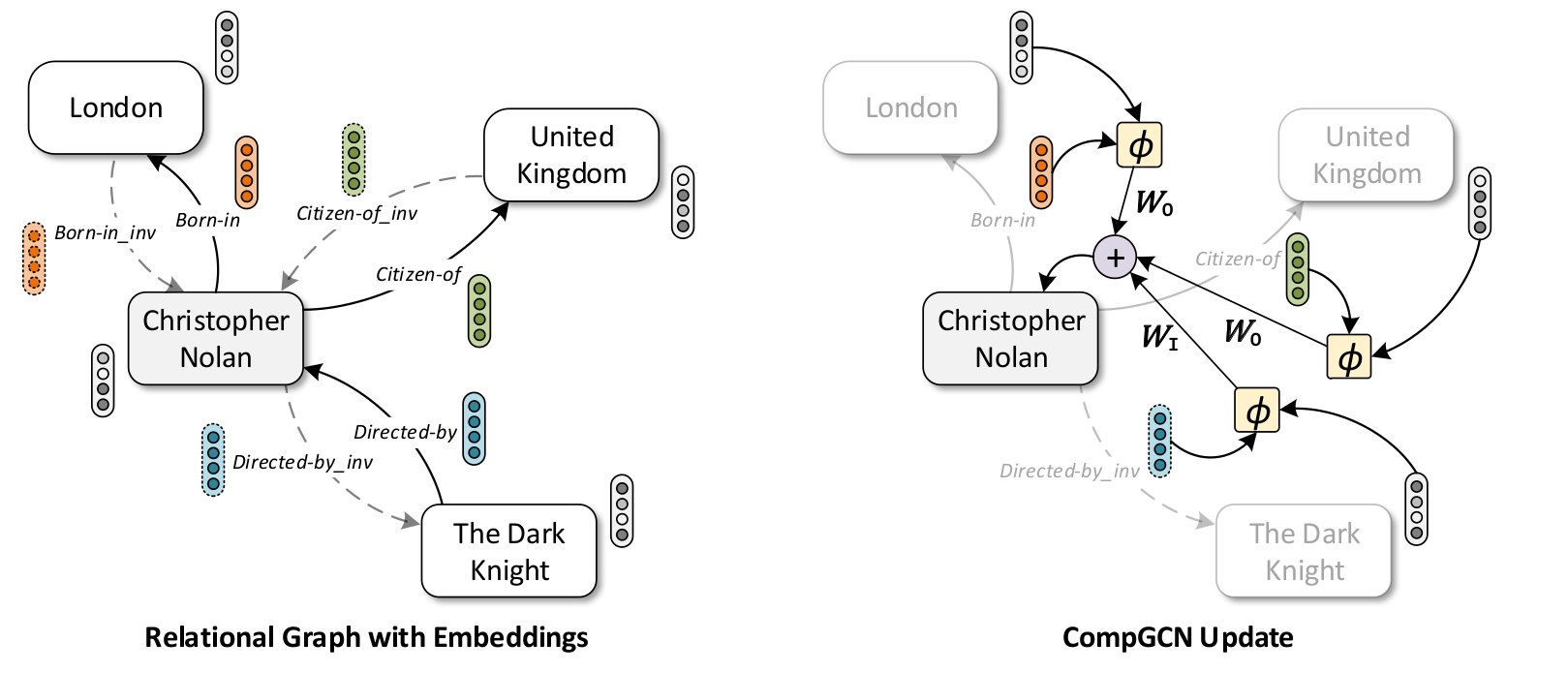
节点更新方式

RGCN （Modeling Relational Data with Graph Convolutional Networks）将 GCN 应用在了知识图谱上 GCN 对于节点 $v$ 的主要更新思想为：

$$\boldsymbol{h}_{v}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{r} \boldsymbol{h}_{u}\right)$$

在 RGCN 中，隐状态 （hidden state）$h_u$ 代表 $v$ 的邻居节点 $u$ 的嵌入表示，它们被赋予初始值 $h^0 = x^0$ 并在计算过程中更新迭代。CompGCN 与 RGCN 的节点更新方式不同，首先我们定义 $h_u,x_u,z_r$，其中 $z_r$ 为节点 $v$ 与邻居节点 $u$ 之间关系的嵌入表示初始值（$r$ 表示关系类型 edge relation type，每种 edge relation type 都被定义了一个单独的嵌入表示 $z_r$），$x_u$ 为邻居节点初始向量，隐状态 $h_u$ 通过 $h_u=\phi (x_u,z_r)$ 来计算。

隐状态 $h_u$​ 经过 $\boldsymbol{W}_{\lambda(r)} \in \mathbb{R}^{d_{1} \times d_{0}}$​ 投影加总后便得到了新的点 $v$​ 嵌入表示。​​

$$\boldsymbol{W}_{\lambda(r)}=\left\{\begin{array}{ll} \boldsymbol{W}_{O}, & r \in \mathcal{R} \\ \boldsymbol{W}_{I}, & r \in \mathcal{R}_{i n v} \\ \boldsymbol{W}_{S}, & r=\top_{(\text {self-loop })} \end{array}\right.$$

在完成节点 $v$ 更新后，对节点间关系的嵌入表示进行更新： $h_r=W_{rel}z_r$​​

总结 CompGCN 的节点更新方式如下：

$$\boldsymbol{h}_{v}^{k+1}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{\lambda(r)}^{k} \phi\left(\boldsymbol{h}_{u}^{k}, \boldsymbol{h}_{r}^{k}\right)\right)\\\boldsymbol{h}_{r}^{k+1}=\boldsymbol{W}_{\mathrm{rel}}^{k} \boldsymbol{h}_{r}^{k}$$

其中 $h^0_v,h^0_r$ 为初始值 $x_v,z_r$​。

论文作者对不同的 $\phi$ （composition 方式）进行了测试，其中包括：

$$\begin{array}{l} \text { Subtraction (Sub): } \phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)=\boldsymbol{e}_{s}-\boldsymbol{e}_{r} \text {. }\\ \text { Multiplication (Mult): } \phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)=\boldsymbol{e}_{s} * \boldsymbol{e}_{r} \text {. }\\ \text { Circular-correlation (Corr): } \phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)=\boldsymbol{e}_{s} \star \boldsymbol{e}_{r} \end{array}$$

通过实验发现各个方案的表现效果取决于得分函数（score function），第二与第三种方式整体稍微好一点。

参数分解

类似 RGCN，CompGCN 论文作者也进行了参数分解。不同的是 RGCN 是对矩阵参数 $W$ 分解，而 CompGCN 则对嵌入向量进行分解： $\boldsymbol{z}_{r}=\sum_{b=1}^{\mathcal{B}} \alpha_{b r} \boldsymbol{v}_{b}$，整体的模型参数数量相对减少了：​

相关图片

(图：CompGCN 与不同模型的参数数量复杂度对比)

实验结果

link prediction

首先 CompGCN 在 link prediction 任务上的大部分指标都超过了表中其他模型。

相关图片

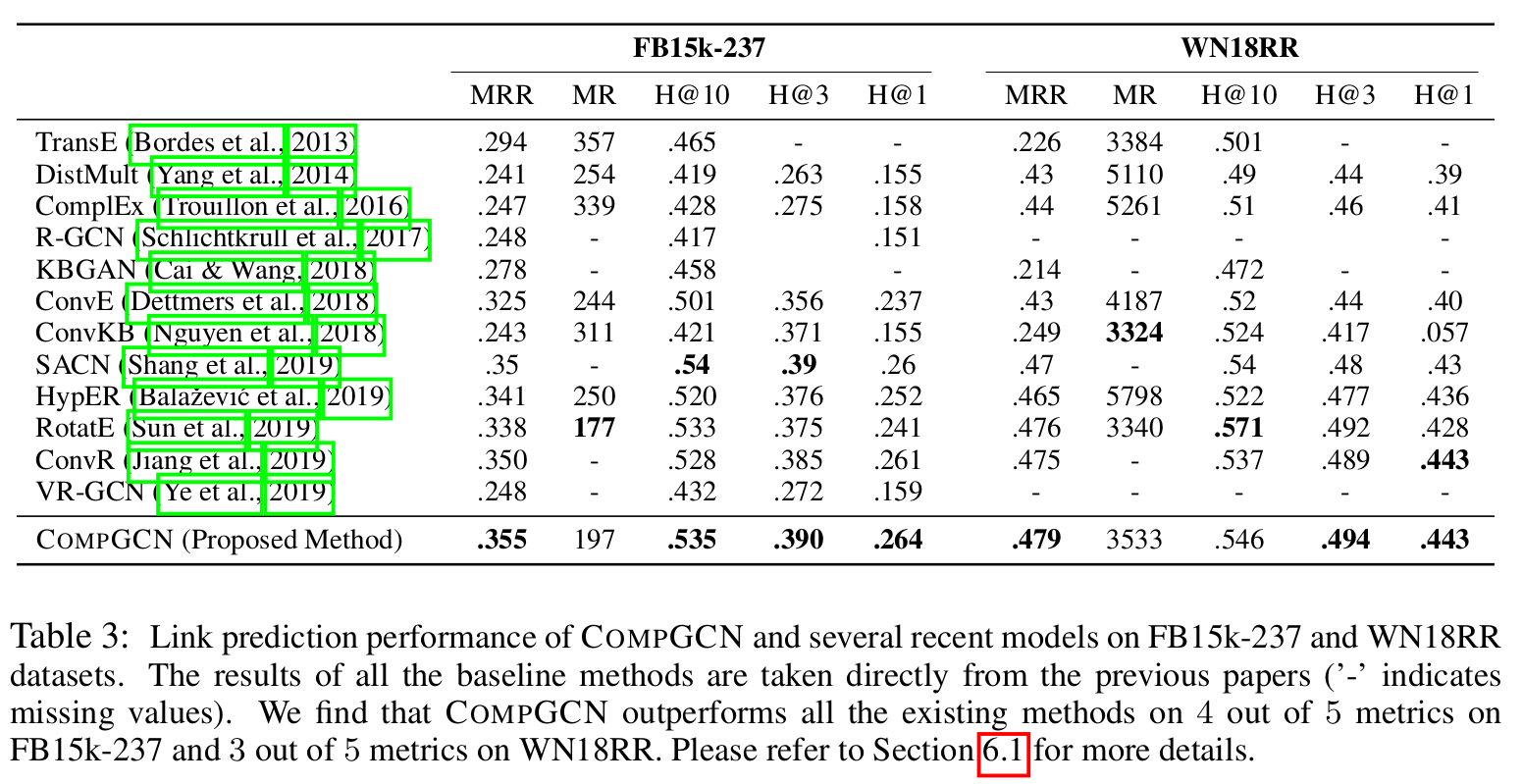
从下表中可以看出，采用了 ConvE 作为 Score function，corr 作为 $\phi$ 函数时的表现最佳。 DistMult 配合 Mult 也不错。

相关图片

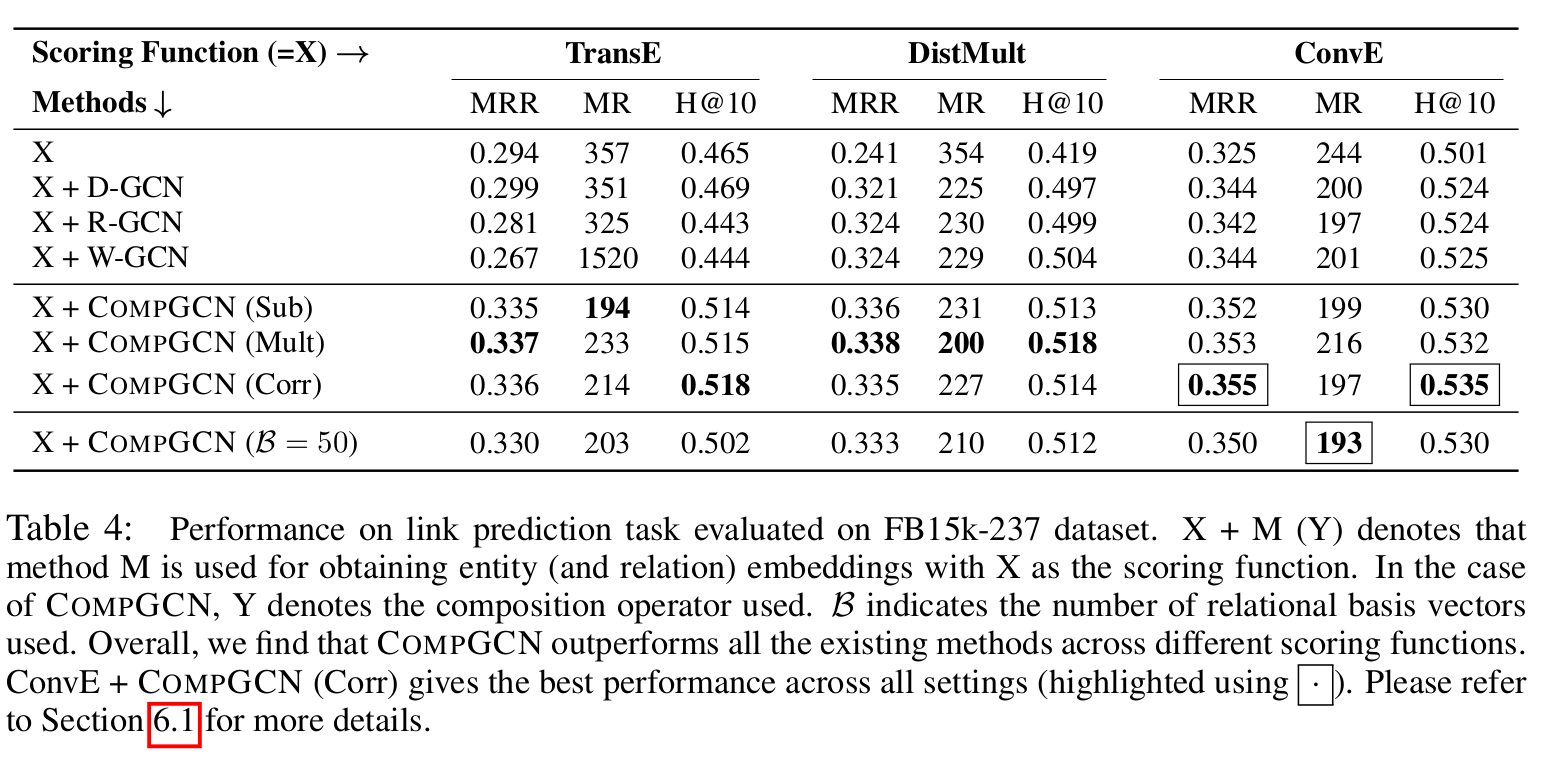
Node and Graph Classification

相关图片

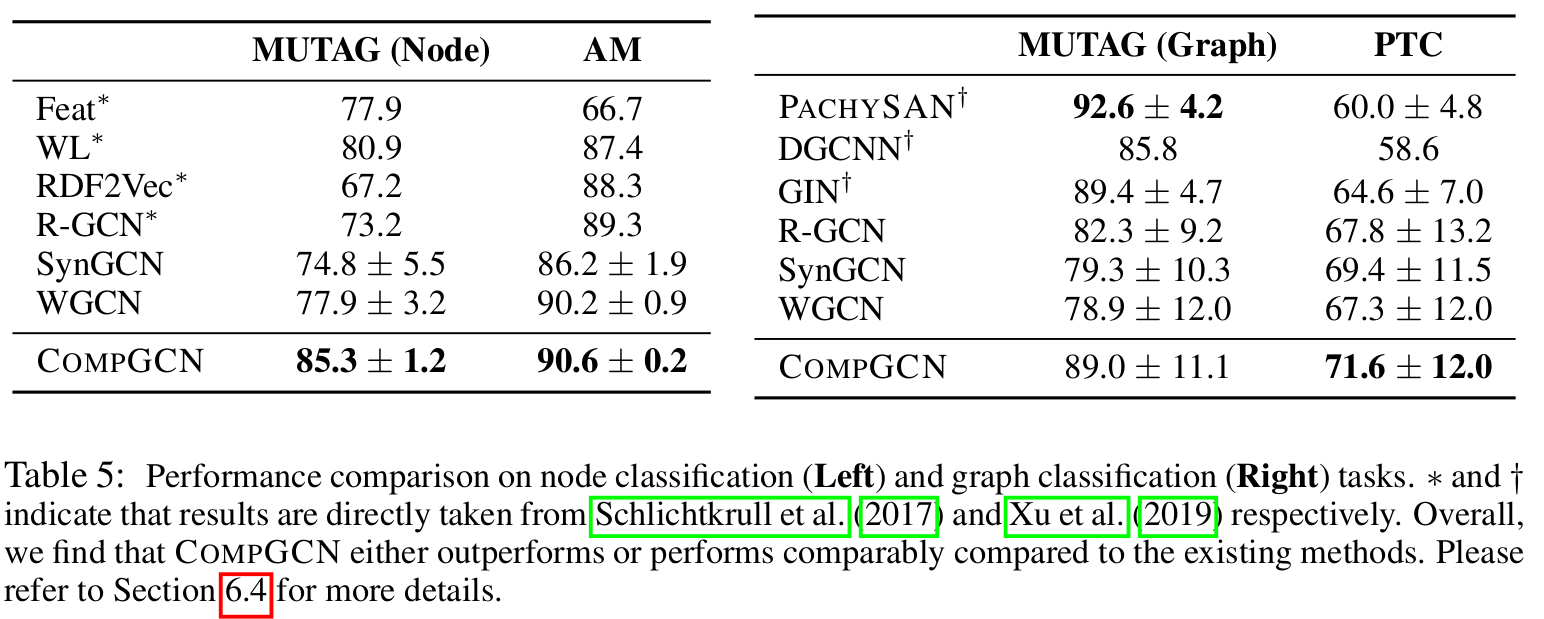
作者似乎没有建议 number of relations 和 basis vectors 两个超参如何选值。不过根据论文相关实验结果，似乎 B=50，number of relations=100 表现较为出色。

KGNN

KGNN 出自 Knowledge-aware Graph Neural Networks with Label Smoothness Regularization for Recommender Systems，其研究了图神经网络在基于知识图谱的推荐系统上的应用与优化。该模型主要用来发现用户可能喜欢，但之前从未接触、浏览过的商品。

首先，论文定义了：

• 用户集 $U$，商品集 $V$
• 由用户隐形反馈（点击，观看，购买等）构成的用户与商品的交互集 $Y$​，也就是训练时候需要用的 ground truth。
• 知识图谱：$G=\{(h,r,t)\}$ ，与大部分图谱定义相似，$h,t$ 代表头尾两个节点，$r$ 代表节点关系类型。​

模型架构

image-20210827162550408

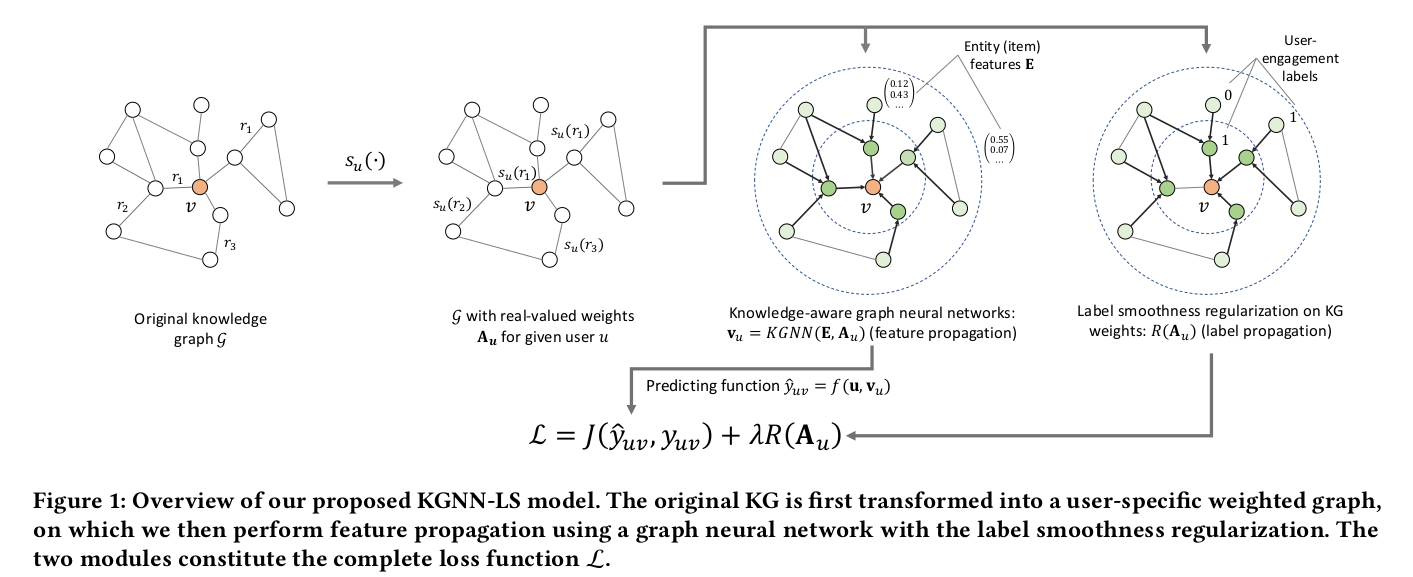
KGNN-LS 的节点的更新方式与 GCN 相似，为：

$$\mathbf{H}_{l+1}=\sigma\left(\mathbf{D}_{u}^{-1 / 2} \mathbf{A}_{u} \mathbf{D}_{u}^{-1 / 2} \mathbf{H}_{l} \mathbf{W}_{l}\right), l=0,1, \cdots, L-1$$

其中 $A_u$​ 为用户 $u$ “专属“ 邻接矩阵（针对不同用户，邻接矩阵不同）， $A^{ij}_u = s_u(r_{e_i,e_j})$ 由 $i, j$ 两个节点的关系 $r_{e_i,e_j}$ 和打分函数 $s_u()$ 决定。$D_u^{ij}$ 为 $A$ 的度矩阵。最终输出 $\mathbf{H}_{L} \in \mathbb{R}^{|\mathcal{E}| \times d_{L}}$​ 可以理解为所有节点（商品与商品属性）对于用户 $u$ 的特征表示。在预测用户 $u$ 对商品 $v$ 评分时使用： $\hat y_{uv} = f(u,v_u)$。其中 $v_u\in H_L$，即我们采用模型最后一层输出的 hidden state 作为节点表示进行计算​​​ 。

两个打分函数 $s(r), f(·)$​ 均为可导函数，如内积。对于 $s(r)$ 甚至可以加入可学习参数，使得我们的邻接矩阵 $A_u$ 能够更好的表现用户特点。

优化目标

$$\min _{\mathbf{W}, \mathrm{A}} \mathcal{L}=\min _{\mathbf{W}, \mathrm{A}} \sum_{u, v} J\left(y_{u v}, \hat{y}_{u v}\right)+\lambda R(\mathrm{~A})+\gamma\|\mathcal{F}\|_{2}^{2}$$

在分类任务下对模型进行优化，其中 $J$ 为交叉熵损失，$||\mathcal{F}||^2_2$ 为 l2 正则， $R(A)$为 label smoothness，与传统的标签平滑方式有点小不同，此处的 $R(\mathbf{A})=\sum_{u} R\left(\mathbf{A}_{u}\right)=\sum_{u} \sum_{v} J\left(y_{u v}, \hat{l}_{u}(v)\right)$ 其中 $\hat l_u(v)$​​​ 为：

$$\hat l_u(v) = l_{u}^{*}=\underset{l_{u}: l_{u}(v)=y_{u v}, \forall v \in \mathcal{V}}{\arg \min } E\left(l_{u}, \mathrm{~A}_{u}\right)$$

$$E\left(l_{u}, \mathbf{A}_{u}\right)=\frac{1}{2} \sum_{e_{i} \in \mathcal{E}, e_{j} \in \mathcal{E}} A_{u}^{i j}\left(l_{u}\left(e_{i}\right)-l_{u}\left(e_{j}\right)\right)^{2}$$

作者在实验中尝试了$\lambda \in 0,0.01,0.1,0.5,1,5$​ ，发现使用 label smoothness 可以很好的提升模型效果，0.1 与 0.01 两个值效果最佳。同时作者在论文中也给出了 label smothness 的相关数学推导，以证明这样的 label smoothness 方式是有效果的，具有可解释性的。(关于这部分可以参考论文具体计算与证明)

相关图片

(图：KGNN-LS 算法伪代码)

实验结果

image-20210827162441690

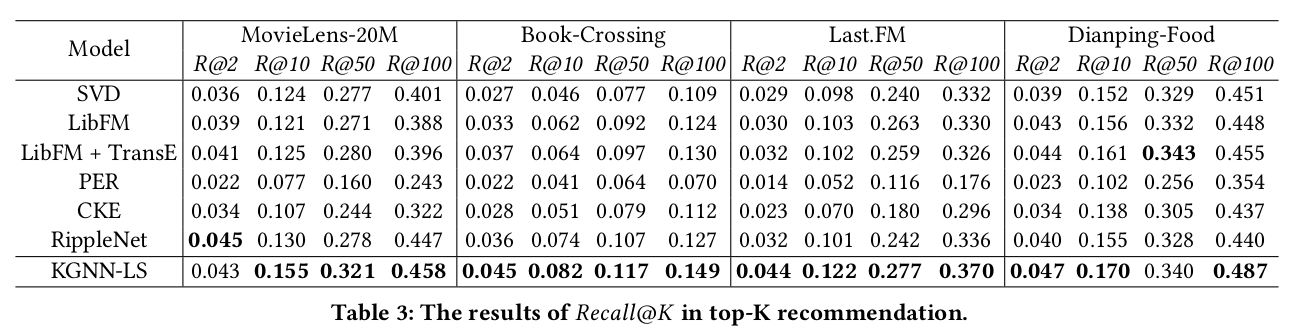
（图：KGNN-LS 基于几个推荐系统数据集的测试结果）