谈谈那些图网络模型 - Monet、EGCN、GraphSage

几何模型 (geometric models) 研究已经在图像处理、流形学习、信号处理等领域得到了广泛的关注。最近几年也有不少的基于 非欧几里德结构数据 深度学习研究。本文主要对 Monet、EGCN、GraphSage 等模型进行总结。

Monet

Mixture model networks (MoNet) 出自 Geometric deep learning on graphs and manifolds using mixture model cnns [1] 一文。他的主要思想是：可学习的核函数。

该论文对先前的几何模型做了总结，如下表。可以看出，大部分几何权重函数都是固定的。

image-20210823202618977

针对上述情况，Monet 作者认为可以从节点之间的边权重入手，来优化模型。于是提出了以下层与层之间的传播方式：

$$D_{j}(x) f=\sum_{y \in \mathcal{N}(x)} w_{j}(\mathbf{u}(x, y)) f(y), \quad j=1, \ldots, J$$

其中，$f(y)$为原节点特征，$w_j(u)$ 为一个包含可学习参数的核函数 kernel。

实验与结果

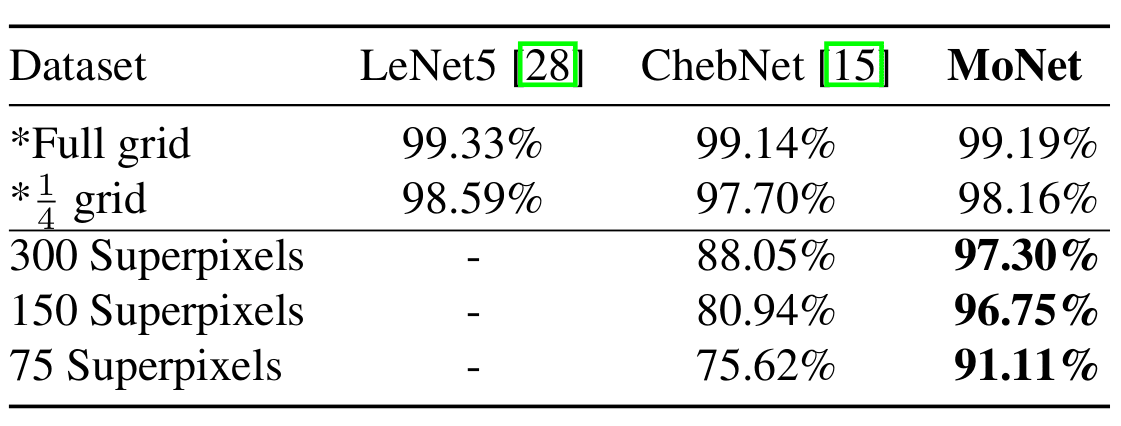
论文作者使用了以下核函数对 MNIST 数据集进行了测试。

$$w_{j}(\mathbf{u})=\exp \left(-\frac{1}{2}\left(\mathbf{u}-\boldsymbol{\mu}_{j}\right)^{\top} \boldsymbol{\Sigma}_{j}^{-1}\left(\mathbf{u}-\boldsymbol{\mu}_{j}\right)\right)$$

结果发现，尽管对于正规网格像素组成的图片，准确率并没有多大提升。但对于超像素构成的图片，MoNet 仍然可以保留很高的准确率。

相关图片

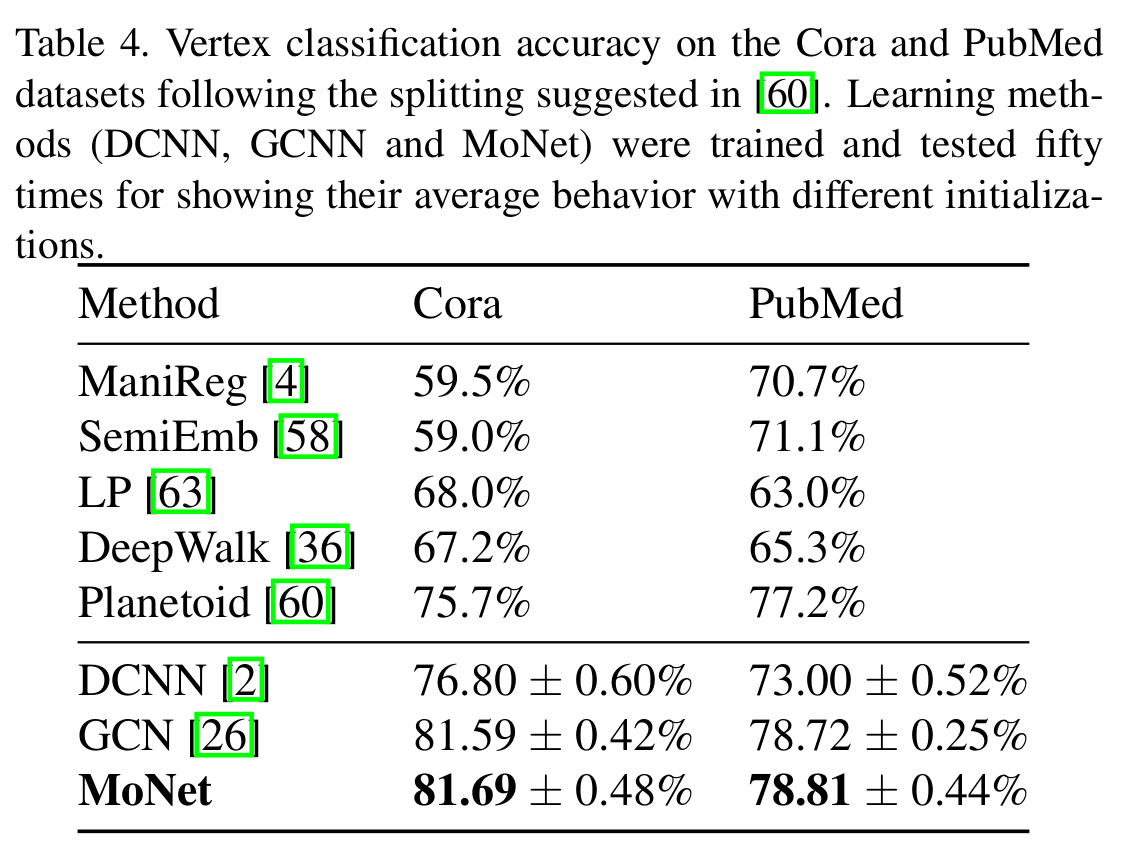
而后作者在 Cora 和 Pubmed 两个数据集上进行了图结构数据的测试。

图模型上的传递方式为：

$$D_{j}(x) f_{l}=\sum_{y \in \mathcal{N}(x)} e^{-\frac{1}{2}\left(\tilde{\mathbf{u}}(x, y)-\boldsymbol{\mu}_{j}\right)^{\top} \boldsymbol{\Sigma}_{j}^{-1}\left(\tilde{\mathbf{u}}(x, y)-\boldsymbol{\mu}_{j}\right)} f_{l}(y)$$

通过对比 GCN 与 DCNN，不难看出可学习的核函数带来了一点点的提升。

相关图片

为啥 MoNet 没 GAT 出名

GAT 与 MoNet 十分相似，也可以说 GAT 是 MoNet 的一个特殊例子，然而两篇论文的被引用数量却差了快 8 倍。

读完 MoNet 的文章，第一感觉是这文章讨论的很全面，不仅在数学方面上对历年的模型做了很好的总结与分析，对于几个不同的研究方向（图片识别，图数据网络，流形学习）也都进行了充分的实验。尽管 GMM 核函数的实验结果好，但在可解释性上似乎还差那么一点。GAT 则着重推广了相对简单的，可解释性相对高一点的方案。另一方面 MoNet 团队的名气确实也不如 Benjio，作为创新者的名气没有后来者高确实可惜。

EGNN

EGNN 出自 Exploiting Edge Features in Graph Neural Networks 一文。其主要思想与特点为：

• 采用多维的正边特征（GAT 只能处理 binary 的边特征，GCN 智能处理一维的边特征）
• 使用新的架构来在层与层之间传递边信息。
• 采用双正则优化，提高训练效果与稳定性。
• 使用多通道编码单向图边信息。

对于以下的解释，我们先定义：

• $X_{ij}$ 表示 第 i 个节点的第 j 个特征
• $E_{i j} \in \mathbb{R}^{P}$表示 i，j 两个节点间 edge 的特征。如果两个节点间没有边的话，则 $E_{ij} = 0$。
• $N_i$​ 为节点 i 的邻居节点。

双正则优化

边特征作为输入前，将会被进行双正则化。操作如下： $\hat E$ 代表原始边特征。

$$\begin{array}{l} \tilde{E}_{i j p}=\frac{\hat{E}_{i j p}}{\sum_{k=1}^{N} \hat{E}_{i k p}} \\ E_{i j p}=\sum_{k=1}^{N} \frac{\tilde{E}_{i k p} \tilde{E}_{j k p}}{\sum_{v=1}^{N} \tilde{E}_{v k p}} \end{array}$$

经过双正则化之后的边为非负值，且不论从 i,或者 j 节点求和，值都为 1。

$$\begin{array}{c} E_{i j p} \geq 0 \\ \sum_{i=1}^{N} E_{i j p}=\sum_{j=1}^{N} E_{i j p}=1 \end{array}$$

EGNN(A)

基于注意力机制的 EGNN 架构

论文提到 GAT 只考虑到了一维的 0/1 遍特征（有边的节点之间存在注意力，没有边的节点不存在注意力。），因此 GAT 的注意力机制由两个节点决定，并没有考虑到边的特征，如边的权重。

EGNN 提出了新的节点前向传导方式：

$$X^{l}=\sigma\left[||_{p=1}^{P}\left(\alpha_{. \cdot p}^{l}\left(X^{l-1}, E_{. . p}^{l-1}\right) g^{l}\left(X^{l-1}\right)\right)\right]$$

其中，

$$g^{l}\left(X^{l-1}\right)=W^{l} X^{l-1}\tag 8$$

注意力系数 $\alpha^l$​ 在 p 通道的切片表示为 $\alpha^l_{..p}$​ ，两个节点之间的注意力系数由 $X^{l-1}_i,X^{l-1}_j,E_{ij}$ 决定。

对于多维度的边特征（$E_{i j} \in \mathbb{R}^{P},p>1$​），每个维度都会引导一个独立的注意力操作，最终的结果由所有维度下计算结果 拼接 得到。

每一个边特征维度的注意力计算方式如下：

$$\hat{\alpha}_{i j p}^{l}=f^{l}\left(X_{i \cdot}^{l-1}, X_{j \cdot}^{l-1}\right) E_{i j p}^{l-1}\\ f^{l}\left(X_{i \cdot}^{l-1}, X_{j \cdot}^{l-1}\right)=\exp \left\{\mathrm{L}\left(a^{T}\left[W X_{i \cdot}^{l-1} \| W X_{j \cdot}^{l-1}\right]\right)\right\}$$

其中 $L$ 为 leakyRelu，$W$ 与(8) 中的映射矩阵相同。计算求得的注意力权重也会被设置为新的边特征：

$$E^l = \alpha^l$$

EGNN(C)

基于卷积的 EGNN 架构。EGNN(C)网络层的传播方式定义为：

$$X^{l}=\sigma\left[||_{p=1}^{P}\left(E_{. . p} X^{l-1} W^{l}\right)\right]$$

对于有向图，EGNN 将将边信息编码成了：

$$[E_{ijp}, E_{jip}, E_{ijp}+E_{jip}]$$

即：前向，反向，无向三种邻居的边信息。

实验结果

从论文结果看出，EGNN(C) 在 Cora， CiteSeer，Pubmed 三个数据记上均优于 GAT 与 GCN。而 EGNN(A) 的评测指标略低于 EGNN(C)。

GraghSage

GraphSAGE(SAmple and aggreGatE) 出自 Inductive Representation Learning on Large Graphs 一文。不同与 GCN，GraphSage 为 inductive 算法，对于新增节点的计算比较友善。同时算法时间复杂度较低，效果也不错，是现在工业界较为流行的一个算法之一。

官方提供的代码链接：tensorflow , pytorch

image-20210824134543213

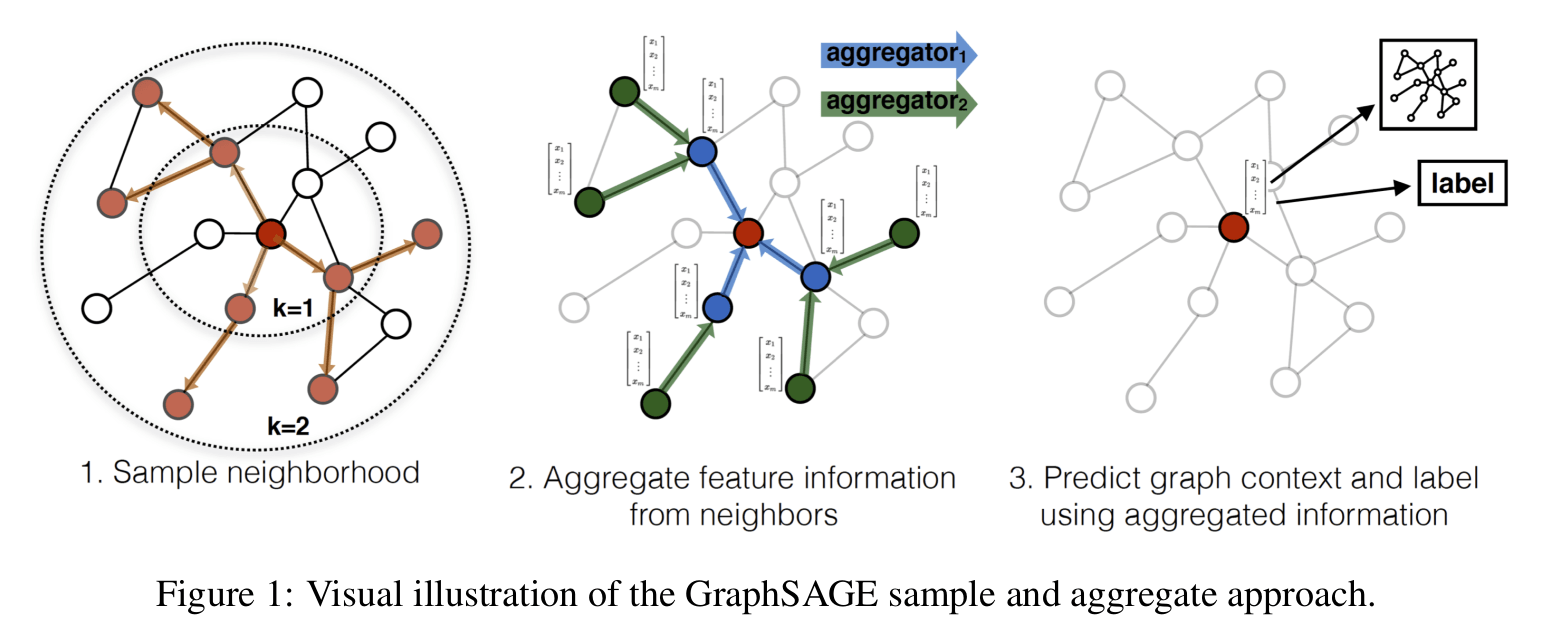
主要算法

他的主要算法如下：

image-20210824135137711

minibatch 的算法

相关图片

采样与邻居的定义

对于采样深度 $K$，与采样个数 $S$，论文作者实验发现 $K=2$ ，$S_1·S_2<500$​ 的效果很好。

采样深度 $K=2$​ 表示，采样时最多对二阶邻居进行采样。当第一层邻居的采样结束后再对第二层邻居进行采样。每一层的采样数量都是固定的（第 $i$​ 层的采样数量为 $S_i$​）。 如果邻居样本数量不够，那么直接以所有邻居节点作为样本即可 （通过下文的聚合方式可以看出，如果使用重复采样的话的出来的结果几乎一样）。

对比 deep walk，graphsage 整个算法复杂度大大减小，其优化就在于这边的随机采样的方式。

优化对象

对于无监督学习，可以采用：

$$J_{\mathcal{G}}\left(\mathbf{z}_{u}\right)=-\log \left(\sigma\left(\mathbf{z}_{u}^{\top} \mathbf{z}_{v}\right)\right)-Q \cdot \mathbb{E}_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-\mathbf{z}_{u}^{\top} \mathbf{z}_{v_{n}}\right)\right)$$

这样做的直觉是拉近邻居节点的表示，拉开非邻居节点之间的表示。Q 为负采样样本的数量，

对于有标签的监督学习，可以采用交叉熵，根据中新节点进行分类学习。

聚合 Aggregate

文中提出了以下聚合方式：

Mean aggregator

GraphSAGE-mean 将算法 1 伪代码中的 4 行替换为了以下操作：

$$\mathbf{h}_{v}^{k} \leftarrow \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{k-1}\right\} \right).$$

伪代码第 5 行的拼接操作可以看做是一次残差连接，使得模型有更好的学习能力。

论文在实验过程中对比了 根据 GCN 推导的 inductive variant 版本（GraphSAGE-GCN），即将算法一伪代码 4-5 行替换为：

$$\mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{k-1}\right\} \cup\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}\right)\right.$$

但从实验结果看来，缺少了残差链接的 GraphSAGE-GCN 总体上效果不如 GraphSAGE-mean

Pooling aggregator

$$\text { AGGREGATE }_{k}^{\text {pool }}=\max \left(\left\{\sigma\left(\mathbf{W}_{\text {pool }} \mathbf{h}_{u_{i}}^{k}+\mathbf{b}\right), \forall u_{i} \in \mathcal{N}(v)\right\}\right)$$

Mean Aggregator 不同的是，Pooling aggregator 使用了可学习的参数。作者发现 mean pooling 和 max pooling 的实验结果并没有太大差异。

LSTM aggregator

LSTM 会由于输入的顺序变化而产生不同输出，这与图网络的性质不符合。对于一个节点来说，他的邻居节点的顺序是并不能为他本身提供有价值的信息。

因此，论文作者在进行节点输入之前，对邻居进行了随机排序，来尽可能减小由于顺序带来的影响。

实验与结果

image-20210824154520815

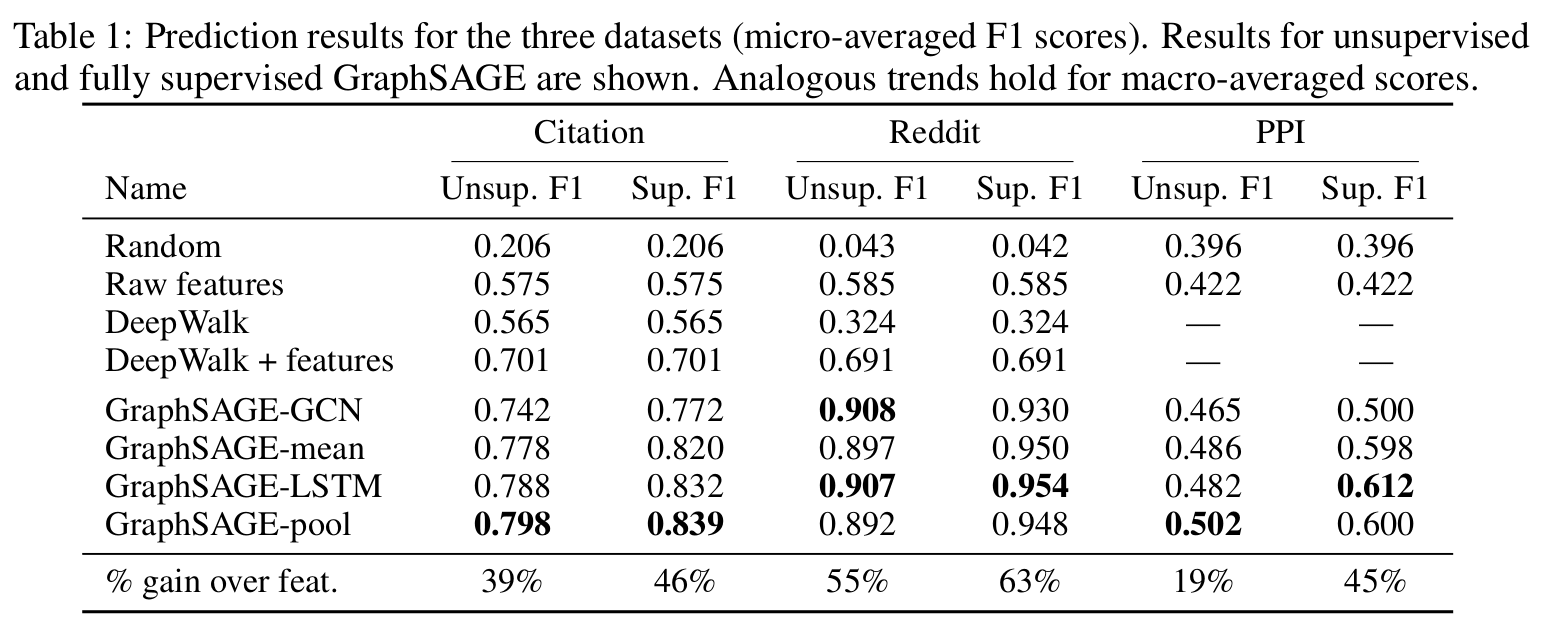
从三个数据集的 Micro-averaged F1 可以看出， GraphSage-pool 与 GraphSAGE-LSTM 的效果更好一些。

image-20210824154652002

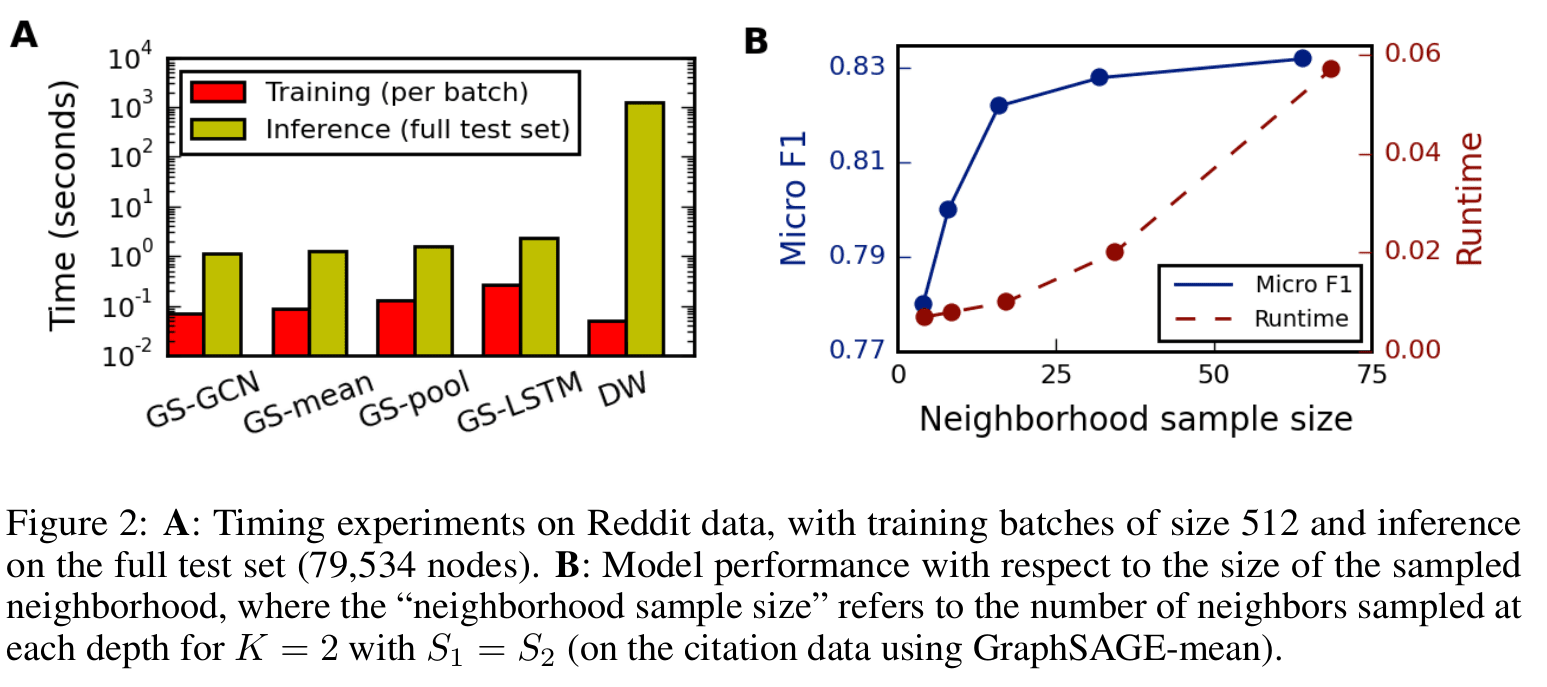
对于训练效率，GraphSAGE 之间的差距并不大，但是他们均比 DeepWalk 快了 2 个数量级。

部分代码细节

首先是 aggregator 的前向传导 pytorch 代码：

def forward(self, nodes, to_neighs, num_sample=10):
    """
    nodes --- list of nodes in a batch
    to_neighs[len()=len(nodes)] --- list of sets, each set is the set of neighbors for node in batch
    num_sample --- number of neighbors to sample. No sampling if None.
    """
    # Local pointers to functions (speed hack)
    _set = set
    if not num_sample is None:
        _sample = random.sample
        samp_neighs = [_set(_sample(to_neigh, 
                        num_sample,
                        )) if len(to_neigh) >= num_sample else to_neigh for to_neigh in to_neighs]
    else:
        samp_neighs = to_neighs

    if self.gcn:
        samp_neighs = [samp_neigh + set([nodes[i]]) for i, samp_neigh in enumerate(samp_neighs)]
    unique_nodes_list = list(set.union(*samp_neighs))
    unique_nodes = {n:i for i,n in enumerate(unique_nodes_list)}
    mask = Variable(torch.zeros(len(samp_neighs), len(unique_nodes)))
    column_indices = [unique_nodes[n] for samp_neigh in samp_neighs for n in samp_neigh]   
    row_indices = [i for i in range(len(samp_neighs)) for j in range(len(samp_neighs[i]))]
    mask[row_indices, column_indices] = 1
    # mask[batch_size, num_unique_sample]
    if self.cuda:
        mask = mask.cuda()
    num_neigh = mask.sum(1, keepdim=True)
    mask = mask.div(num_neigh) # 得到每个 batch 的权重。
    if self.cuda:
        # 此处 features 为 nn.Embedding()
        embed_matrix = self.features(torch.LongTensor(unique_nodes_list).cuda())
    else:
        embed_matrix = self.features(torch.LongTensor(unique_nodes_list))
    to_feats = mask.mm(embed_matrix)
    return to_feats

算法 1 伪代码中的第 5 行对应的就是下面 encoder 部分的前向推导代码：

def forward(self, nodes):
    """
    Generates embeddings for a batch of nodes.
    nodes     -- list of nodes
    """
    neigh_feats = self.aggregator.forward(nodes, [self.adj_lists[int(node)] for node in nodes], self.num_sample)
    if not self.gcn: 
        # 论文中有提出，如果使用类似 GCN 的 inductive 方式，不会有拼接操作。
        if self.cuda:
            self_feats = self.features(torch.LongTensor(nodes).cuda())
        else:
            self_feats = self.features(torch.LongTensor(nodes))
        combined = torch.cat([self_feats, neigh_feats], dim=1)
    else:
        combined = neigh_feats
    combined = F.relu(self.weight.mm(combined.t()))
    return combined

于是整个网络的可以定义成：

class SupervisedGraphSage(nn.Module):

    def __init__(self, num_classes, enc):
        super(SupervisedGraphSage, self).__init__()
        self.enc = enc
        self.xent = nn.CrossEntropyLoss()

        self.weight = nn.Parameter(torch.FloatTensor(num_classes, enc.embed_dim))
        init.xavier_uniform(self.weight)

    def forward(self, nodes):
        embeds = self.enc(nodes)
        scores = self.weight.mm(embeds)
        return scores.t()

    def loss(self, nodes, labels):
        scores = self.forward(nodes)
        return self.xent(scores, labels.squeeze())

因为 K=2，所以在创建类实例的时候可以采用以下方式：

num_nodes = 2708
feat_data, labels, adj_lists = load_cora()
features = nn.Embedding(2708, 1433)
features.weight = nn.Parameter(torch.FloatTensor(feat_data), requires_grad=False)
# features.cuda()

agg1 = MeanAggregator(features, cuda=True)
enc1 = Encoder(features, 1433, 128, adj_lists, agg1, gcn=True, cuda=False)
# 在对二阶邻居计算完成后，使用对应节点的新特征进行计算。
# 这边新的 features 包含了原节点 features 与其二阶邻居聚合后的信息
agg2 = MeanAggregator(lambda nodes : enc1(nodes).t(), cuda=False)
enc2 = Encoder(lambda nodes : enc1(nodes).t(), enc1.embed_dim, 128, adj_lists, agg2,
               base_model=enc1, gcn=True, cuda=False)
enc1.num_samples = 5
enc2.num_samples = 5

graphsage = SupervisedGraphSage(7, enc2)

参考

1. Monet：Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodolà, Jan Svoboda, and Michael MBronstein. Geometric deep learning on graphs and manifolds using mixture model cnns. arXiv preprint arXiv:1611.08402, 2016.
2. Gong, L., & Cheng, Q. (2019). Exploiting edge features for graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 9211-9219).
3. Hamilton, W. L., Ying, R., & Leskovec, J. (2017, December). Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems (pp. 1025-1035).