机械学习| HMM CRF 简笔
HMM/CRF 笔记 机器学习-白板推导系列(十四)-隐马尔可夫模型 HMM机器学习-白板推导系列(十七)-条件随机场 CRF
HMM
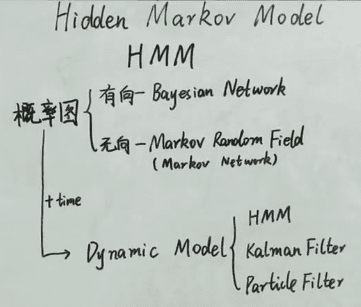
对于静态图,样本之间是独立同分布的:。 HMM 属于概率图中的动态模型,x 之间并不是独立的。
如对于一个 GMM 静态图 ,有 。若加上时间则生成序列(称为动态模型):
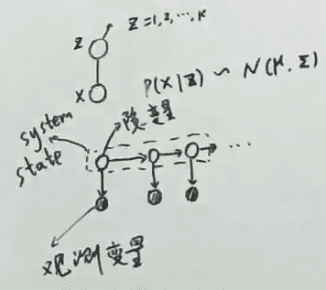
图例中,上方为 GMM 静态图,下方为动态图, 横向代表时间 , 纵向代表混合 。图中阴影 为观测变量, 观测变量 有对应的 隐状态 ,这些隐状态通称为 系统状态 。
动态度可继续划分,系统状态是离散的话,则模型为 HMM;若状态是连续的,线性的为 Kalman 滤波,非线性的为 Particle 滤波。
HMM 模型:
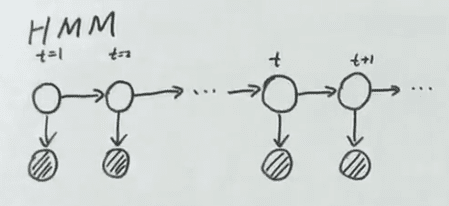
图中阴影变量为观测变量 ,状态空间 白圈为状态变量 ,状态空间 。
HMM 模型可表示为: 其中转移矩阵为
发射矩阵为 。
HMM 假设
齐次 Markov 假设 :当前状态 仅 与前一状态有关
观测独立假设 :当前观测变量 仅 与当前对应的状态变量有关。
HMM 的三个环节
Learning:如何学习模型的参数? Decoding:给定模型参数与观测序列,如何找到一个状态序列 使得 最大? Evaluation:给定模型所有参数,如何衡量观测序列的概率?
Evaluation
给定 求
基于齐次 Markov 假设:
基于观察独立假设:
暴力算法时间复杂度
前向算法 ():
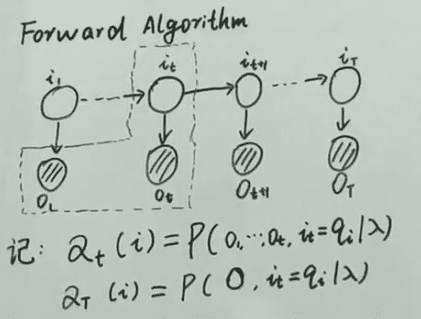
后向算法:
记:
那么:
Learning
问题描述:求解
将 EM 算法应用与 HMM 后得出:
其中 , 与 已知,因此:
在上一节已经求出:
所以:
其中 有 三个参数,以下挑选 进行推导:
HMM 的基础概念中有约束条件:
因此使用拉格朗日乘子法求解:
将 代入 得:
Decoding
解码采用维特比算法:
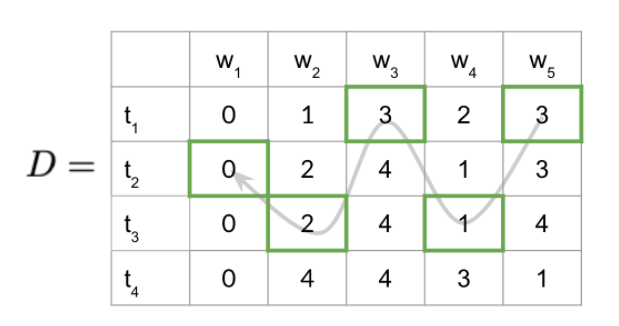
以下使用概率矩阵 与 动作矩阵 来进行辅助解释。其中 为观测变量, 为隐状态。 为状态转移矩阵, 为发射矩阵。
概率矩阵中 记录 。即,对于序列 在 时刻对应的隐状态为 时候的最大概率。 时刻之前的隐状态没有条件限制。
动作矩阵中 记录:对于序列 , 时刻对应的隐状态为 概率最大时, 时刻隐状态为 。
- 初始化概率矩阵 与 动作矩阵 。
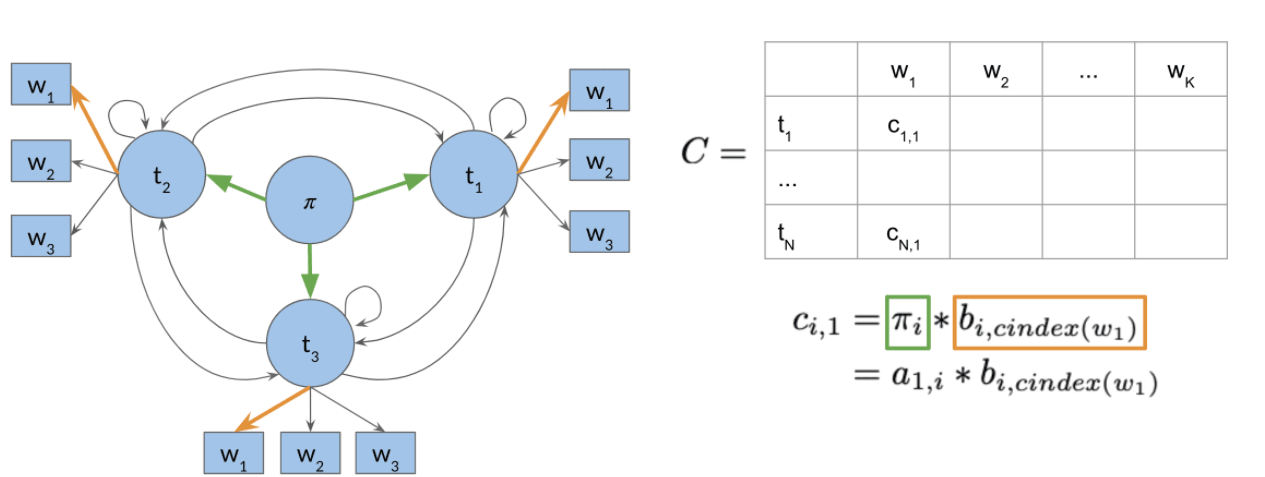
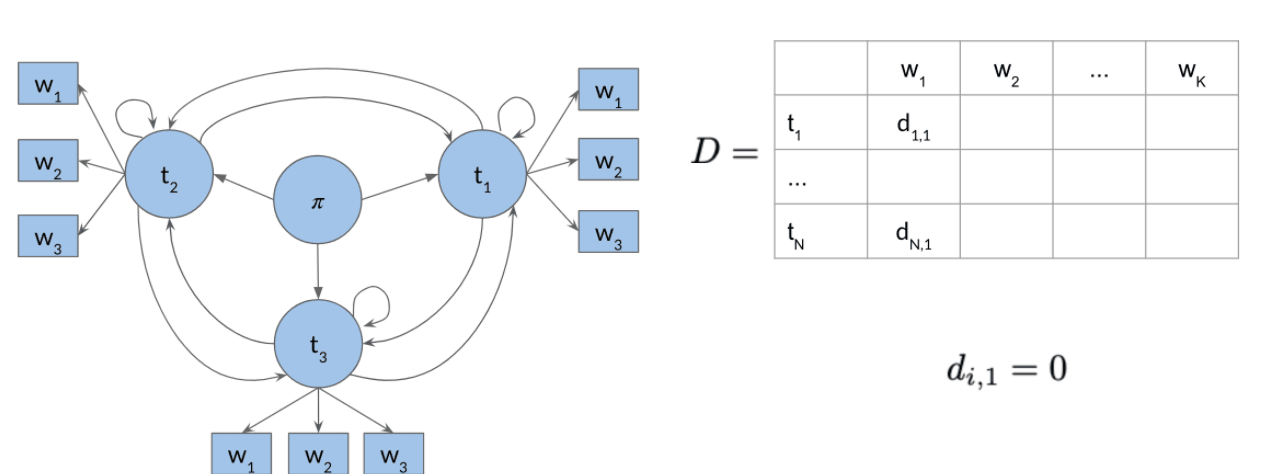
- 前向推导,填充满 两个矩阵。
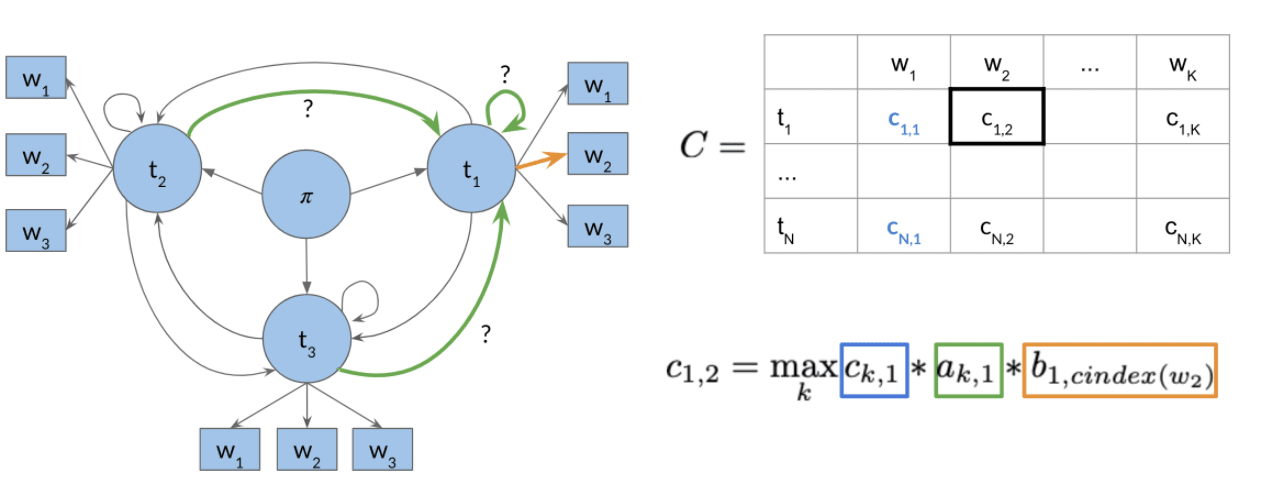
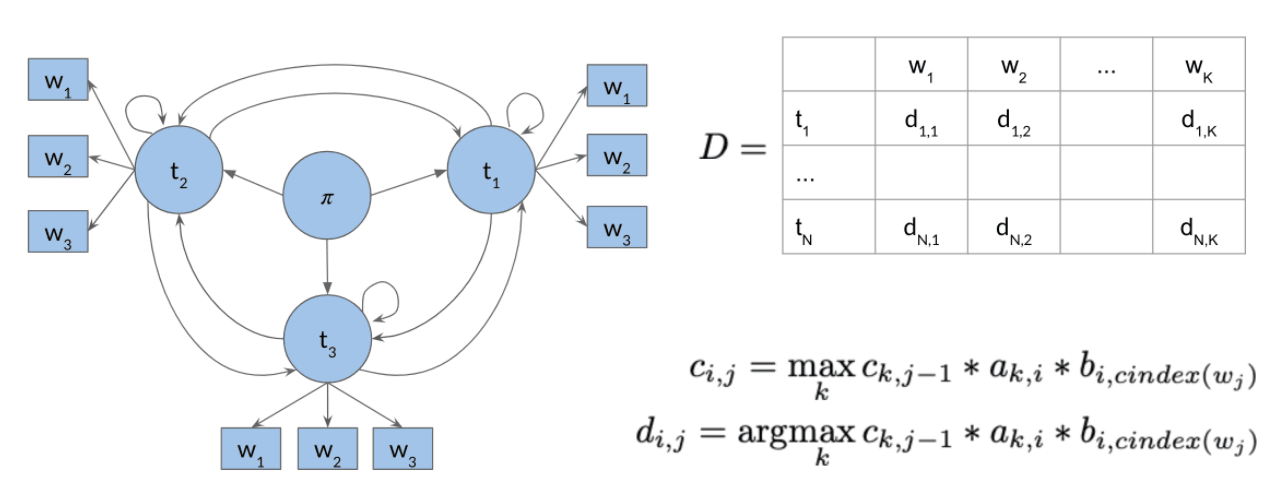
- 反向推导。
CRF
对于解决分类问题,模型可以分为硬模型(输出为类似 01 的确认值)与软模型(输出为概率)。
软模型可以再分为: 概率生成模型(对 建模)。如朴素贝叶斯、HMM。 概率判别模型(对 )进行建模。如 MEMM、CRF
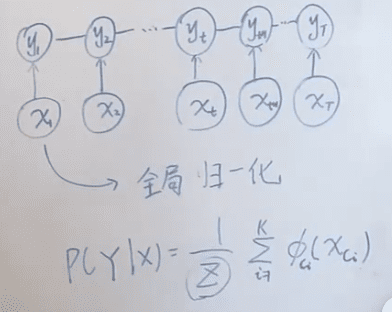
CRF 概率图如下,打破了 HMM 的观测独立假设,即 会受到 的影响:
随机场: 当给每一个位置中按照某种分布随机赋予相空间的一个值之后,其全体就叫做随机场。
马尔科夫随机场:
马尔科夫随机场及由马尔科夫性质的随机场,它指的是一个随机变量序列按时间先后关系依次排开的时候,第 N+1 时刻的分布特性,与 N 时刻以前的随机变量的取值无关。(比如今天天气仅与昨天有关,与前天...无关)
线性条件随机场 CRF
通常 NLP 中的 CRF 默认为线性链条件随机场。如同马尔科夫随机场,条件随机场为无向图模型。不同的是,CRF 具有给定的观测变量 。
线性链条件随机场中 与 结构相同。
线性链条件随机场分解:
根据 Hammersley-Clifford 定理,马尔科夫随机场可以分解为:
是无向图的最大团, 联合概率分布,为势函数。通常指定势函数为指数函数,因此:
根据 CRF 的概率图表示,有:
其中
为转移函数(类似 HMM 转移矩阵)
为状态函数(类似 HMM 发射矩阵)。
其中 , 为给定的特征函数。对状态及转移的可能性进行限制。而 是需要学习的参数。
因此 CRF 的概率函数总结为:
CRF 简化表示
定义 ,
因此:
其中 为归一化因子。
参数学习 Learning
学习的目标是
即:
采用梯度下降/梯度上升法进行优化即可。
解码 Decoding
解码采用维特比算法,与 HMM 部分的维特比算法相似。