跳至主要內容

机械学习|降维

Kevin 吴嘉文大约 6 分钟知识笔记Machine Learning

线性回归基础数学。笔记思路源于 shuhuai-白板机械学习open in new window 系列教程。

降维

维度灾难

特征数量的增加并不能保证模型效果更上一层楼，大量的特征可能导致样本稀疏率的增加，进而导致过拟合。 在高纬度的情况下，样本之间的欧式距离趋向于无法区分大小：

lim⁡d→∞dist⁡max⁡−dist⁡min⁡dist⁡min⁡→0 \lim _{d \rightarrow \infty} \frac{\operatorname{dist}_{\max }-\operatorname{dist}_{\min }}{\operatorname{dist}_{\min }} \rightarrow 0

从几何角度讲:

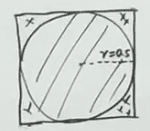
image-20220315111212079
image-20220315111212079

设二维空间下正方形边长为 1，则其内切圆半径为 0.5，因此球体的体积为 k(0.5)Dk(0.5)^D ，正方体体积为 1。当维度 DD 增加时，内切超球体体积趋近于零。假设二维空间下的正方体四个角落对应四个类别的样本。在高维空间下，样本稀疏性变大，分类变得困难。

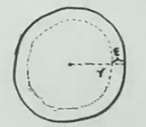
image-20220315111720027
image-20220315111720027

设外圆半径 r=1r=1 ，内圆半径为 r−ϵr-\epsilon 。 在高维情况下，外圆体积为 k1D=kk1^D=k，中间圆环体积为 k−k(1−ϵ)Dk - k(1-\epsilon)^D 。当 DD 趋近于无穷大时，中间环的体积趋近于 kk，内圆体积趋近于零。因此，高维情况下，环形带占据了几乎整个外圆，就像大脑一样，所有知识分布在大脑皮层上。因此在平面或三维几何上的一些直觉，在高维空间上是不起作用的。

为了解决过拟合，通常使用个的是增加数据量量、正则化和降维。L1 和 L1 两种正则化方法，本质也是为了降维：增加系数惩罚，使得 ww 趋向于零，以此消除一些特征。

样本均值与样本方差的矩阵表示

样本均值表示为：

Xˉ=1N∑i=1Nxi=1N(x1x2⋯xN)(11⋮1)=1NXT1N \bar{X}=\frac{1}{N} \sum_{i=1}^{N} x_{i}=\frac{1}{N}\left(\begin{array}{llll} x_{1} & x_{2} & \cdots & x_{N} \end{array}\right)\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)=\frac{1}{N} X^{T} 1_{N}

样本方差表示为：

Sp×p=1N∑i=1N(xi−Xˉ)(xi−Xˉ)T=1N(x1−Xˉx2−Xˉ⋯xN−Xˉ)((x1−Xˉ)T(x2−Xˉ)T⋮(xN−Xˉ)T)=1N((x1x2⋯xN)−Xˉ⋅1NT)((x1Tx2T⋮xNT)−1N⋅XˉT)=1N(XT−Xˉ⋅1NT)(X−1N⋅XˉT)=1N(XT−1NXT1N1NT)(X−1N1N1NTX)=1NXT(IN−1N1N1NT)(IN−1N1N1NT)X \begin{array}{l} S_{p \times p}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{X}\right)\left(x_{i}-\bar{X}\right)^{T}\\ =\frac{1}{N}\left(\begin{array}{llll} x_{1}-\bar{X} & x_{2}-\bar{X} & \cdots & x_{N}-\bar{X} \end{array}\right)\left(\begin{array}{c} \left(x_{1}-\bar{X}\right)^{T} \\ \left(x_{2}-\bar{X}\right)^{T} \\ \vdots \\ \left(x_{N}-\bar{X}\right)^{T} \end{array}\right)\\ =\frac{1}{N}\left(\left(\begin{array}{llll} x_{1} & x_{2} & \cdots & x_{N} \end{array}\right)-\bar{X} \cdot 1_{N}^{T}\right)\left(\left(\begin{array}{c} x_{1}^{T} \\ x_{2}^{T} \\ \vdots \\ x_{N}^{T} \end{array}\right)-1_{N} \cdot \bar{X}^{T}\right)\\ =\frac{1}{N}\left(X^{T}-\bar{X} \cdot 1_{N}^{T}\right)\left(X-1_{N} \cdot \bar{X}^{T}\right)\\ =\frac{1}{N}\left(X^{T}-\frac{1}{N} X^{T} 1_{N} 1_{N}^{T}\right)\left(X-\frac{1}{N} 1_{N} 1_{N}^{T} X\right)\\ =\frac{1}{N} X^{T}\left(I_{N}-\frac{1}{N} 1_{N} 1_{N}^{T}\right)\left(I_{N}-\frac{1}{N} 1_{N} 1_{N}^{T}\right) X \end{array}

此处 INI_N 为 N×NN \times N 的单位矩阵，令 IN−1N1N1NTI_{N}-\frac{1}{N} 1_{N} 1_{N}^{T} 为 HH （centering matrix）

H 矩阵有以下性质：

HT=(IN−1N1N1NT)T=(IN−1N1N1NT)=HH2=H \begin{array}{l} H^{T}=\left(I_{N}-\frac{1}{N} 1_{N} 1_{N}^{T}\right)^{T}=\left(I_{N}-\frac{1}{N} 1_{N} 1_{N}^{T}\right)=H \\ H^{2}=H \end{array}

因此 S=1NXTHHX=1NXTHXS=\frac{1}{N} X^{T} H H X=\frac{1}{N} X^{T} H X

PCA

主成分分析主要思想为：

一个中心： 对原始特征空间的重构，将相关的特征转为无关的特征。将特征空间变成一组相互正交的基。

两个基本点：

  • 最大投影方差：找到投影轴，使得投影后方差最大。
  • 最小重构距离：以最小的代价将投影后的数据重构回去。

数学推导

从最大化投影方差出发：

  • 数据中心化 xi′=xi−xˉx_{i}^{\prime}=x_{i}-\bar{x}
  • 将 x′x' 投影到 u1u_1

假设 ∥u1∥=1\left\|u_{1}\right\|=1 ， 即 u1Tu1=1u_{1}^{T} u_{1}=1

projection =∥x′∥cos⁡θ=\left\|x^{\prime}\right\| \cos \theta ( θ\theta 为 x′x^{\prime} 与 u1u_{1} 的夹角)

x′⋅u1=∥x′∥∥u1∥cos⁡θ=∥x′∥cos⁡θx^{\prime} \cdot u_{1}=\left\|x^{\prime}\right\|\left\|u_{1}\right\| \cos \theta=\left\|x^{\prime}\right\| \cos \theta

又因为 x′⋅u1=x′Tu1x^{\prime} \cdot u_{1}=x^{\prime T} u_{1}

所以 projection =x′Tu1=x^{\prime T} u_{1}

由于 x′x^{\prime} 已经中心化, 其均值为 0 , 因此投影方差为 (x′Tu1)2\left(x^{\prime T} u_{1}\right)^{2}

  • 目标函数

J=1N∑i=1N((xi−xˉ)Tu1)2 s.t. u1Tu1=1J=1N∑i=1Nu1T(xi−xˉ)(xi−xˉ)Tu1=u1T(1N∑i=1N(xi−xˉ)(xi−xˉ)T)u1 \begin{aligned} J &=\frac{1}{N} \sum_{i=1}^{N}\left(\left(x_{i}-\bar{x}\right)^{T} u_{1}\right)^{2} \text { s.t. } u_{1}^{T} u_{1}=1 \\ J &=\frac{1}{N} \sum_{i=1}^{N} u_{1}^{T}\left(x_{i}-\bar{x}\right)\left(x_{i}-\bar{x}\right)^{T} u_{1} \\ &=u_{1}^{T}\left(\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)\left(x_{i}-\bar{x}\right)^{T}\right) u_{1} \end{aligned}

其中 1N∑i=1N(xi−xˉ)(xi−xˉ)T)\left.\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)\left(x_{i}-\bar{x}\right)^{T}\right) 为协方差矩阵 SS, 因此:

J=u1TSu1 J=u_{1}^{T} S u_{1}

u^1=argmax⁡u1TSu1s.t. u1Tu1=1 \hat{u}_{1}=\operatorname{argmax} u_{1}^{T} S u_{1}\\ s.t.\ u_{1}^{T} u_{1}=1

使用拉格朗日乘子法：

 令 L(u1,λ)=u1TSu1+λ(1−u1Tu1) \text { 令 } L\left(u_{1}, \lambda\right)=u_{1}^{T} S u_{1}+\lambda\left(1-u_{1}^{T} u_{1}\right)

∂L∂u1=2Su1−2λu1=0Su1=λu1 \frac{\partial L}{\partial u_{1}}=2 S u_{1}-2 \lambda u_{1}=0\\ S u_{1}=\lambda u_{1}

从公式可以看出，u1u_{1} 为 SS 的特征向量， λ\lambda 为对应的特征值。 这也解释了为啥 PCA 要算特征向量与特征值。

从 SVD 看 PCA

将 XX 左乘中心矩阵 HH 进行中心化后进行奇异值分解：

HX=UΣVT H X=U \Sigma V^{T}

其中 UU 为 N×NN \times N， VV 为 p×pp \times p 且 VTV=IV^TV = I

结合第二节的结论：S=1NXTHXS=\frac{1}{N} X^{T} H X

S=1NXTHTHX=1N(HX)THX=(UΣVT)TUΣVT=VΣTUTUΣVT=VΣTΣVT \begin{aligned} S &=\frac{1}{N} X^{T} H^{T} H X \\ &=\frac{1}{N}(H X)^{T} H X \\ &=\left(U \Sigma V^{T}\right)^{T} U \Sigma V^{T} \\ &=V \Sigma^{T} U^{T} U \Sigma V^{T} \\ &=V \Sigma^{T} \Sigma V^{T} \end{aligned}

因此 VV 是 SS 的特征向量，中心化 X 后的 SVD 结果等价于上一节 PCA 的结果。

PCA 步骤

  • 数据中心化 X -= mean(X)
  • 计算协方差矩阵 Cov(X)=1mXTXCov(X) = \frac 1m X^TX
  • 计算特征向量，特征值为 λ\lambda ，则：

det⁡(∑−λI)=0λ(1001)=(λ  00  λ) det (S11−λ  S12S21  S22−λ)=0(s11−λ)(s22−λ)−s21s12=0 \begin{array}{l} \operatorname{det}\left(\sum-\lambda I\right)=0 \\ \lambda\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)=\left(\begin{array}{l} \lambda\ \ 0 \\ 0\ \ \lambda \end{array}\right) \text { det }\left(\begin{array}{l} S_{11}-\lambda\ \ S_{12} \\ S_{21}\ \ S_{22}-\lambda \end{array}\right)=0 \\ \left(s_{11}-\lambda\right)\left(s_{22}-\lambda\right)-s_{21} s_{12}=0 \end{array}

λ=tr(Cov(x))±tr2(Cov(X))−4det(Cov(X))2\lambda = \frac {tr(Cov(x)) \pm \sqrt{tr^2(Cov(X))-4det(Cov(X))} }{2}

L_1 = (S.trace() + np.sqrt(pow(S.trace(),2) - 4*np.linalg.det(S)))/2
L_2 = (S.trace() + np.sqrt(pow(S.trace(),2) + 4*np.linalg.det(S)))/2
# S is the Cov matrix of X
  • 特征向量计算 (Cayley-Hamilton theory)

II 是 mm 维的单位矩阵；A=Cov(X)−λ∗IA = Cov(X) - \lambda * I；E=A[:,i]norm(A[:,i])E = \frac {A[:,i]} { norm(A[:,i]) }

A1 = S - L_1 * np.identity(2)
A2 = S - L_2 * np.identity(2)
E1 = A2[:,1]
E2 = A1[:,0]
E1 /= np.linalg.norm(E1)
E2 /= np.linalg.norm(E2)
  • 最后，选择前 k 个维度作为主要成分。特征值反应了对应维度的重要性
上次编辑于:
贡献者: kevinng77