跳至主要內容

RLHF|DPO, GRPO

Kevin 吴嘉文大约 4 分钟知识笔记NLPAIGCLLMAgent

本文梳理了 DPO，GRPO 的主要特点、亮点以及相关资源链接。

DPO

论文：Direct preference optimization: Your language model is secretly a reward model. arXiv preprint arXiv:2305.18290, 2023open in new window

先来回顾以下 PPO，采用 PPO 的 RLHF 会经过 reward model tuning 和 Reinforcement Learning 2 个步骤：

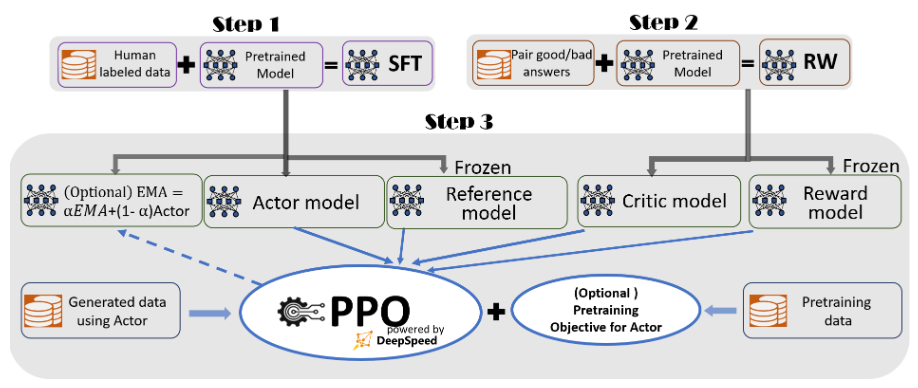
image-20240804094219585
image-20240804094219585

首先在上图的 Step 2 中训练 reward model r(s,a)r(s,a)，优化正负样本之间的距离

LR(rϕ,D)=−E(x,yw,yl)∼D[log⁡σ(rϕ(x,yw)−rϕ(x,yl))] \mathcal{L}_R(r_{\phi}, \mathcal{D}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( r_{\phi}(x, y_w) - r_{\phi}(x, y_l) \right) \right]

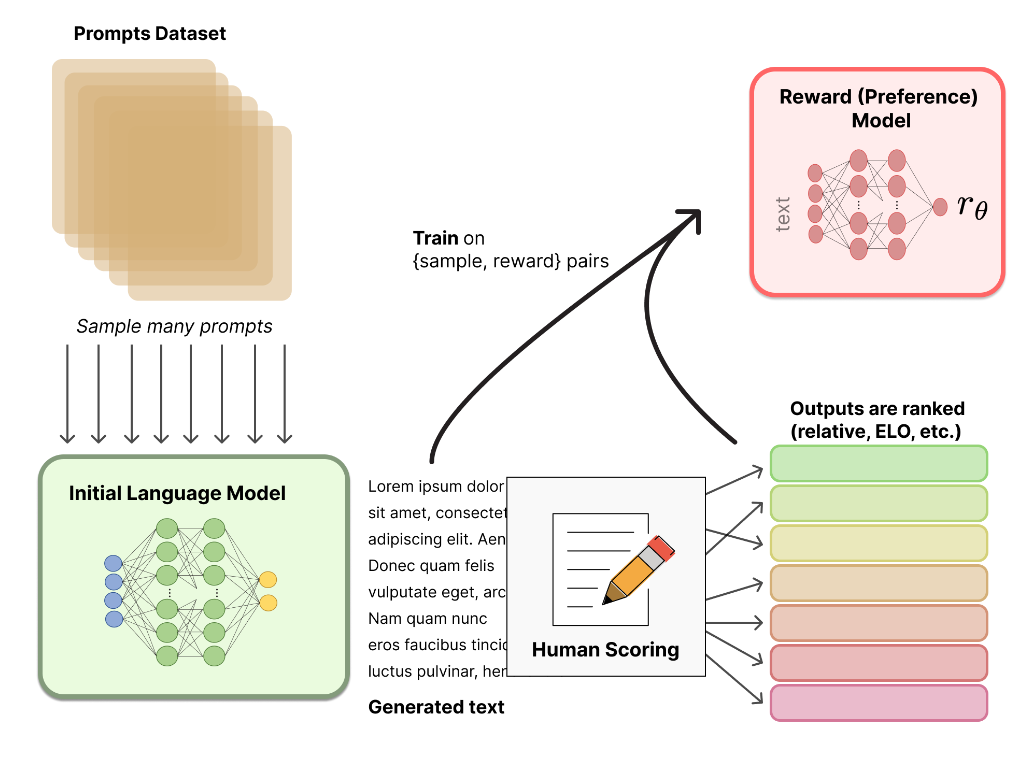
image-20240804095337710
image-20240804095337710

而后在 Step 3 中采用梯度上升优化 LLM，目标函数为：

max⁡πθEx∼D,y∼πθ(y∣x)[rϕ(x,y)]−βDKL[πθ(y∣x)∥πref(y∣x)] \max_{\pi_{\theta}} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(y | x)} \left[ r_{\phi}(x, y) \right] - \beta \mathbb D_{KL} \left[ \pi_{\theta}(y | x) \parallel \pi_{\text{ref}}(y | x) \right]

大致流程如下：

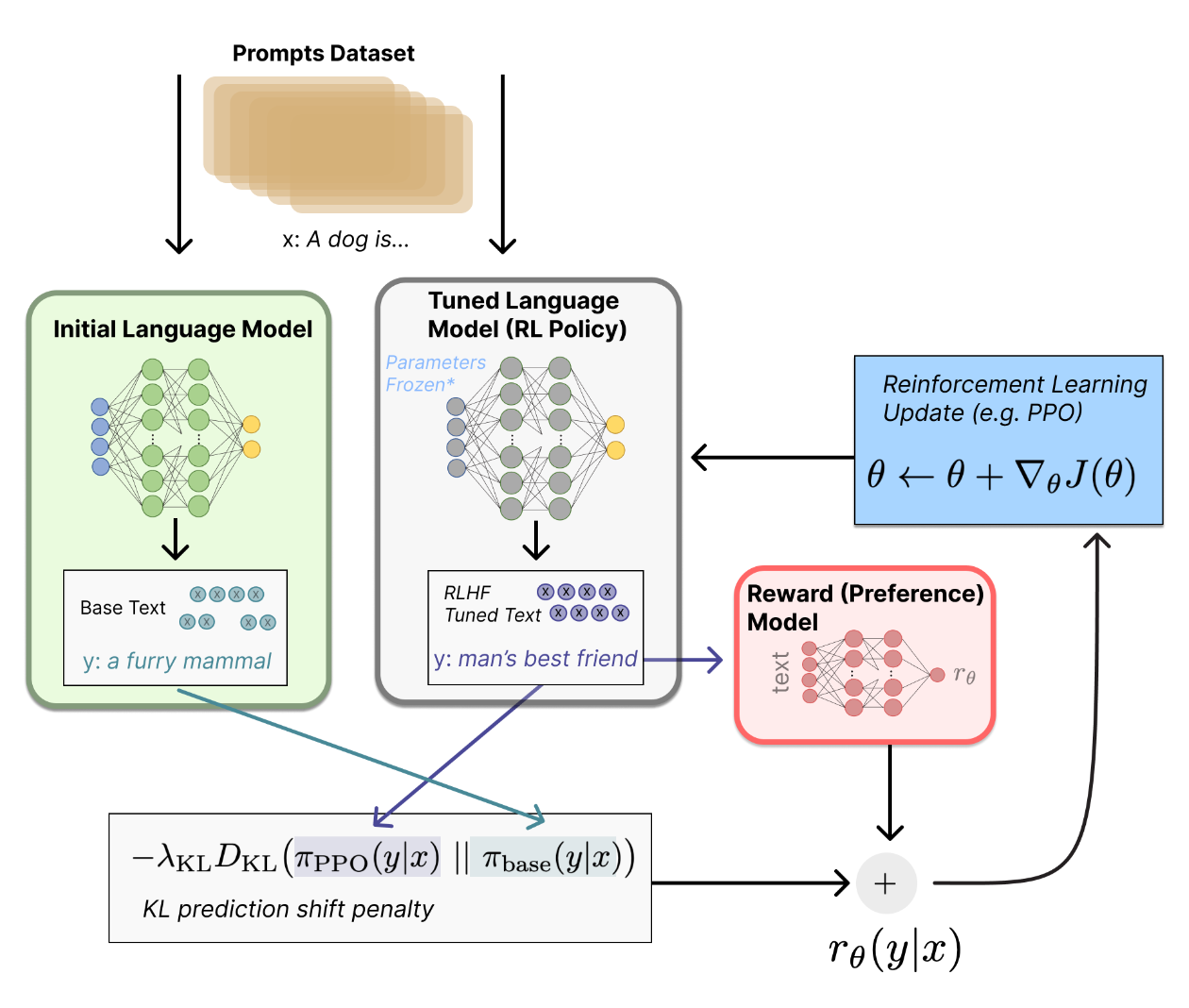
image-20240804095128762
image-20240804095128762

更多 PPO 细节可以参考 RLHF 基础笔记open in new window。

DPO 的重点在于：将 PPO 的目标函数转化为了简单的 binary corss-entropy 目标函数。

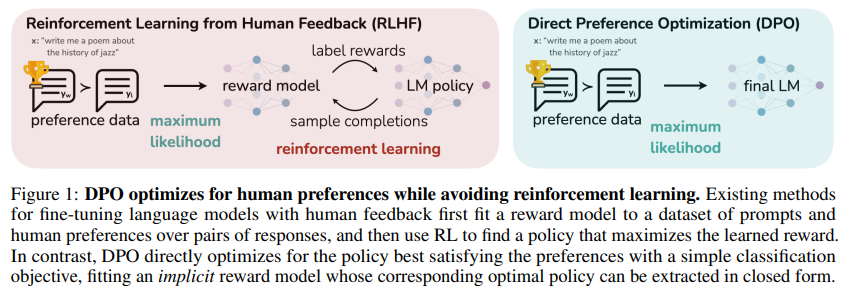
image-20240804100532102
image-20240804100532102

max⁡πθEx∼D,y∼πθ(y∣x)[rϕ(x,y)]−βDKL[πθ(y∣x)∥πref(y∣x)]=max⁡πEx∼DEy∼π(y∣x)[r(x,y)−βlog⁡π(y∣x)πref(y∣x)]=min⁡πEx∼DEy∼π(y∣x)[log⁡π(y∣x)πref(y∣x)−1βr(x,y)]=min⁡πEx∼DEy∼π(y∣x)[log⁡π(y∣x)1Z(x)πref(y∣x)exp⁡(1βr(x,y))−log⁡Z(x)](1) \begin{aligned} &\max_{\pi_{\theta}} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(y | x)} \left[ r_{\phi}(x, y) \right] - \beta \mathbb D_{KL} \left[ \pi_{\theta}(y | x) \parallel \pi_{\text{ref}}(y | x) \right]\\ =& \max_{\pi} \mathbb{E}_{x \sim \mathcal{D}} \mathbb{E}_{y \sim \pi(y | x)} \left[ r(x, y) - \beta \log \frac{\pi(y | x)}{\pi_{\text{ref}}(y | x)} \right]\\ =& \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}} \mathbb{E}_{y \sim \pi(y | x)} \left[ \log \frac{\pi(y | x)}{\pi_{\text{ref}}(y | x)} - \frac{1}{\beta} r(x, y) \right]\\ =& \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}} \mathbb{E}_{y \sim \pi(y | x)} \left[ \log \frac{\pi(y | x)}{\frac{1}{Z(x)} \pi_{\text{ref}}(y | x) \exp \left( \frac{1}{\beta} r(x, y) \right)} - \log Z(x) \right] \end{aligned}\tag 1

其中 Z(x)Z(x) 为 partition function：

Z(x)=∑yπref(y∣x)exp⁡(1βr(x,y)) Z(x) = \sum_y \pi_{\text{ref}}(y | x) \exp \left( \frac{1}{\beta} r(x, y) \right)

我们可以定义：

π∗(y∣x)=1Z(x)πref(y∣x)exp⁡(1βr(x,y)), \pi^*(y | x) = \frac{1}{Z(x)} \pi_{\text{ref}}(y | x) \exp \left( \frac{1}{\beta} r(x, y) \right),

于是公式 (1)(1) 可以整理成：

min⁡πEx∼D[Ey∼π(y∣x)[log⁡π(y∣x)π∗(y∣x)]−log⁡Z(x)]=min⁡πEx∼D[DKL(π(y∣x)∥π∗(y∣x))−log⁡Z(x)] \begin{aligned} \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}} \left[ \mathbb{E}_{y \sim \pi(y | x)} \left[ \log \frac{\pi(y | x)}{\pi^*(y | x)} \right] - \log Z(x) \right] &= \\ \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}} \left[ D_{KL}(\pi(y | x) \parallel \pi^*(y | x)) - \log Z(x) \right] \end{aligned}

可以看到，上式中，Z(x)Z(x) 是不受 π\pi 能影响的。因此当 KL 散度为 0 时，以上式子有最优解，即：

π(y∣x)=π∗(y∣x)=1Z(x)πref(y∣x)exp⁡(1βr(x,y)) \pi(y | x) = \pi^*(y | x) = \frac{1}{Z(x)} \pi_{\text{ref}}(y | x) \exp \left( \frac{1}{\beta} r(x, y) \right)

但以上式子中，Z(x)Z(x) 比较难求，因此我们对上式进行以下变换，可以得到：

r(x,y)=βlog⁡πr(y∣x)πref(y∣x)+βlog⁡Z(x) r(x, y) = \beta \log \frac{\pi_r(y | x)}{\pi_{\text{ref}}(y | x)} + \beta \log Z(x)

将以上式子带入，reward function 的损失函数中，得到：

LR(rϕ,D)=−E(x,yw,yl)∼D[log⁡σ(rϕ(x,yw)−rϕ(x,yl))]=−E(x,yw,yl)∼D[log⁡σ(βlog⁡πθ(yw∣x)πref(yw∣x)−βlog⁡πθ(yl∣x)πref(yl∣x))]=LDPO(πθ;πref) \begin{aligned} \mathcal{L}_R(r_{\phi}, \mathcal{D}) &= -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( r_{\phi}(x, y_w) - r_{\phi}(x, y_l) \right) \right]\\ &= -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \frac{\pi_{\theta}(y_w | x)}{\pi_{\text{ref}}(y_w | x)} - \beta \log \frac{\pi_{\theta}(y_l | x)}{\pi_{\text{ref}}(y_l | x)} \right) \right]\\ &=\mathcal{L}_{\text{DPO}}(\pi_{\theta}; \pi_{\text{ref}}) \end{aligned}

因此，优化时候采用的数据集格式与训练 reward model 相似，也是 (x,yw,yl)(x,y_w, y_l) 的格式，在优化 LDPO(πθ;πref)\mathcal{L}_{\text{DPO}}(\pi_{\theta}; \pi_{\text{ref}}) 时，不计算 reward model，也可以实现 RLHF 的效果。

参考 trl 的 dpo loss 计算方式，大致流程为：

def dpo_loss(
        self,
        policy_chosen_logps: torch.FloatTensor,
        policy_rejected_logps: torch.FloatTensor,
        reference_chosen_logps: torch.FloatTensor,
        reference_rejected_logps: torch.FloatTensor,
    ) -> Tuple[torch.FloatTensor, torch.FloatTensor, torch.FloatTensor]:
		# ... 省略部分代码
		logits = (policy_chosen_logps - reference_chosen_logps) - (policy_rejected_logps - reference_rejected_logps)
        if self.loss_type == "sigmoid":
        	losses = (
                -F.logsigmoid(self.beta * logits) * (1 - self.label_smoothing)
                - F.logsigmoid(-self.beta * logits) * self.label_smoothing
            )
        # ... 省略其他 loss_type
        return losses, # ... 省略其他输出

在优化时候，可以与 sft loss 一起优化，当同时优化 SFT + DPO 时，sft loss 只计算 chosen 样本对应的 loss。

GRPO

论文：DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Modelsopen in new window

GRPO 在 DeepSeek V2 中采用了，GRPO 在训练过程中，不需要 Value Model，因此也能够减少 RL 训练过程中的资源消耗。

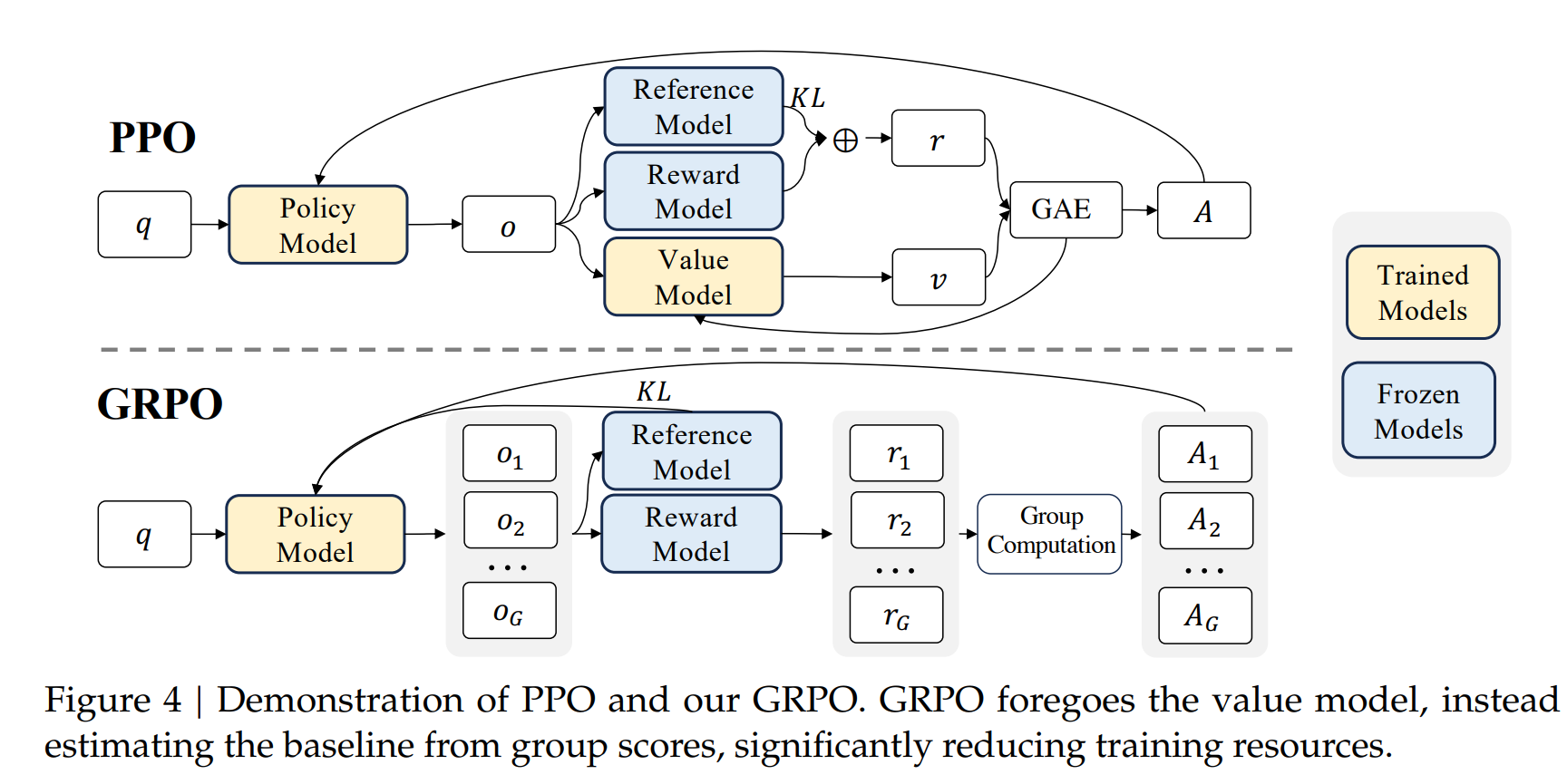
image-20240804164813773
image-20240804164813773

GRPO 的目标函数为：

JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O∣q)][1G∑i=1G1∣oi∣∑t=1∣oi∣{min⁡[πθ(oi,t∣q,oi,<t)πθold(oi,t∣q,oi,<t)A^i,t,clip(πθ(oi,t∣q,oi,<t)πθold(oi,t∣q,oi,<t),1−ϵ,1+ϵ)A^i,t]−βDKL[πθ∥πref]}] \mathcal{J}_{\text{GRPO}}(\theta) = \mathbb{E} \left[ q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q) \right] \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left\{ \min \left[ \frac{\pi_{\theta}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} | q, o_{i,<t})} \hat{A}_{i,t}, \text{clip} \left( \frac{\pi_{\theta}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} | q, o_{i,<t})}, 1 - \epsilon, 1 + \epsilon \right) \hat{A}_{i,t} \right] - \beta D_{KL} \left[ \pi_{\theta} \parallel \pi_{\text{ref}} \right] \right\} \right]

GRPO 的步骤大致为：

image-20240804164951112
image-20240804164951112

其中，advantage A^i,t=ri−mean(r)std(r)\hat A_{i,t} = \frac {r_i - mean(r)}{std(r)} 。

参考

RLHF 相关训练代码示例：

  • https://github.com/huggingface/alignment-handbook

  • https://github.com/OpenRLHF/OpenRLHF

  • https://github.com/hiyouga/LLaMA-Factory