DIFFUSION 系列笔记| SDE（上）

论文 SCORE-BASED GENERATIVE MODELING THROUGH STOCHASTIC DIFFERENTIAL EQUATIONS

从 stochastic differential equations 的角度，尝试提出了一个统一的模型框架，来概括 DDPM，SMLD 等 score-based generative models。

该论文的作者 宋飏 在他的博客中也详细地介绍了该模型的理论，并且提供了基于 torch 的 Colab 教程。本文主要基于宋飏的博客，对该论文提出的模型思路进行了重新整理。

相关信息

宋飏大佬的博客从 Score based Model 和 Langivan Dynamic 等理论入手，逐步介绍到了 Diffusion SDE 模型。不同于宋飏博士的原博客，本文主要先记录了 SDE 模型。在了解 SDE 的操作流程后，再继续深入，记录其中的 Langivan Dynamic，score-function 等相关原理。

1. 理论 - 扩散模型和 SDE 的结合

相关信息

在 DDIM 中，其作者对 DDPM 的采样及前项传播公式进行了修改。从而实现了采样的确定性以及速度提升。而在 SDE 中，其作者将扩散模型的前向与反向过程与 [stochastic process](https://en.wikipedia.org/wiki/Stochastic_process#:~:text=A stochastic or random process can be defined as a,an element in the set.) 巧妙地建立了联系。这使得我们能够从物理学地角度出发，用该领域地理论去验证、推理和改进扩散过程。

1.1 Forward Process

我们可以把 diffusion 的前向过程看作 stochastic process （类似布朗运动的随机过程），这里的 diffusion 过程指我们将一张完整图片，一步一步加噪，直至变成完全噪音图片的过程，对这个概念陌生的朋友可以参考 扩散模型探索：DDPM 笔记与思考。

我们定义 $\{\mathbf{x}(t) \in \mathbb{R}^d \}_{t=0}^T$ 为一个 diffusion 前向过程，那么在这个扩散过程中， $x(t)$ 之间的关系可以通过 stochastic differential equation (SDE) 表示为：

$$\begin{aligned} d \mathbf{x} = \mathbf{f}(\mathbf{x}, t) d t + g(t) d \mathbf{w} \end{aligned}\tag1$$

其中 $t \in[0,T]$ 代表时间步，$\mathbf{w}$ 为 standard Wiener process（也称 Brownian motion，可以看作是随机项），$\mathbf{f}(\mathbf{x}, t)$ 和 $g(t)$ 分别为 drift coefficient 和 diffusion coefficient 。在 DDIM 中，我们发现 diffusion 的前向过程可以看作 ODE。SDE 与 ODE 的主要差别在于 SDE 在传播过程中，添加了随即项 $g(t) d \mathbf{w}$ 。

如果用 $p_t(x)$ 表示 $X(t)$ 的分布，通过上面的 diffusion 前向过程，我们能够将一整图片 $x(0) \sim p_0$ 转变成完全的噪声 $x(T) \sim p_T$ 。此处 $p_T$ 也称为 prior distribution，它是一个可以轻松采样得到的分布。

1.2 Backward Process

一个有趣的事情是，对于公式 $(1)$ 的 SDE 过程，我们能够通过数学方式推导出他的逆向过程，即 reverse SDE。reverse SDE 是其他领域的研究成果，并非为扩散模型而生，其推导过程相对复杂，可以参考网友推导 或者 Maruyama_method。我们可以将采用 reverse SDE 作为 diffusion 的反向过程，具体公式为：

$$\begin{aligned} d\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g^2(t)\nabla_{\mathbf{x}}\log p_t(\mathbf{x})] dt + g(t) d\bar{\mathbf{w}} \end{aligned}\tag2$$

其中 $\bar{\mathbf{w}}$ 为反向过程中的 Brownian motion。参考以上公式，我们只需要知道 drift coefficient ，diffusion coefficient 以及 score function $\nabla_{\mathbf{x}}\log p_t(\mathbf{x})$ 就可以进行反向过程了。

img

对于 reverse SDE，我们可以训练一个模型 $s_\theta(\mathbf{x}(t), t)$ 来拟合 score function，训练时候的优化目标来源于 Denoising Score Matching：

$$\begin{aligned} \min_\theta \mathbb{E}_{t\sim \mathcal{U}(0, T)} [\lambda(t) \mathbb{E}_{\mathbf{x}(0) \sim p_0(\mathbf{x})}\mathbf{E}_{\mathbf{x}(t) \sim p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))}[ \|s_\theta(\mathbf{x}(t), t) - \nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))\|_2^2]] \end{aligned}\tag3$$

这与其中 $\lambda(t) \in \mathbb{R}_{>0}$ 为正的权重系数。

参考文章 A Connection Between Score Matching and Denoising Autoencoders ：

$$\nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))=\frac {x(0)-x(t)}{\sigma^2}\tag4$$

其中 $\sigma$ 为 $p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))$ 的方差，将 $(4)$ 式带入到 $(3)$ 式的优化项中得到：

$$\begin{aligned} &\lambda(t) \|s_\theta(\mathbf{x}(t), t) - \nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))\|_2^2\\=&\lambda(t) \|s_\theta(\mathbf{x}(t), t)+\frac z{\sigma}\|_2^2\\ =&\|\sigma \times s_\theta(\mathbf{x}(t), t)+z\|_2^2 \end{aligned} \tag5$$

其中 $z=\frac{x(t)-x(0)}{\sigma}$，$\lambda(t) = \sigma^2$ 。此处，作者令 $\lambda(t) \propto 1 / \mathbb{E}\left[\left\|\nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))\right\|_2^2\right]$ 是为了使得 loss 在不同的时间步 $t$ 下保持平衡。

2. 实践 - 定义 SDE 前向推导

注意！以下前项推导过程基于特定 假设 ，目的是为了简化 SDE 流程，以便学习和理解。 官方的 SDE 系列模型前项推导过程与下文介绍的大同小异，我们会在下一章节讨论到。

假设我们的前向过程为：

$$\begin{aligned} d \mathbf{x} = \beta^t d\mathbf{w}, \quad t\in[0,1] \end{aligned}\tag6$$

在 SDE 原文及源码中，上述公式中可能记为 $d \mathbf{x} = \sigma^t d\mathbf{w}, \quad t\in[0,1]$ 。为避免读者将其中的 $\sigma$ 和方差 $\sigma$ 混淆，因此在本文中我们将其标记为 $\beta$ 。

参考上文的公式 $(1)$，很明显公式 $(6)$ 令 drift coefficient 为 0，在这个情况下

$$\begin{aligned} p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0)) = \mathcal{N}\bigg(\mathbf{x}(t); \mathbf{x}(0), \frac{1}{2\log \beta}(\beta^{2t} - 1) \mathbf{I}\bigg) \end{aligned}\tag7$$

当 $\beta$ 足够大时，先验分布 $p_{01}$ 为：

$$\begin{aligned} \int p_0(\mathbf{y})\mathcal{N}\bigg(\mathbf{x}; \mathbf{y}, \frac{1}{2 \log \beta}(\beta^2 - 1)\mathbf{I}\bigg) d \mathbf{y} \approx \mathbf{N}\bigg(\mathbf{x}; \mathbf{0}, \frac{1}{2 \log \beta}(\beta^2 - 1)\mathbf{I}\bigg) \end{aligned}\tag8$$

这个先验分布就是 $x(1)$ 的分布，在生成图片的过程中，我们需要通过该分布，采样出来 $x(1)$，而后通过反向过程来生成我们想要的图片 $x(0)$。

因此根据公式 $(5)$，loss 的计算过程可以写成：

import paddle
import functools

# Modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=zOsoqPdXHuL5
def loss_fn(model, x, marginal_prob_std, eps=1e-5):
    """Compute the loss function. 参考公式 (5)

    Args:
      model: A score model.
      batch: A mini-batch of training data.

    Returns:
      loss: A scalar that represents the average loss value across the mini-batch.
    """
    # 此处的 score funciton 可以看做是一个 Unet + post processing
    random_t = paddle.rand((x.shape[0],)) * (1. - eps) + eps  
    z = paddle.randn(x.shape)
    std = marginal_prob_std(random_t)
    perturbed_x = x + z * std[:, None, None, None]
    score = model(perturbed_x, random_t)
    
    # 如公式 5 得出 loss 的计算结果。 
    loss = paddle.mean(paddle.sum((score * std[:, None, None, None] + z)**2, axis=(1,2,3)))
    return loss

其中 marginal_prob_std 表示 $p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))$ 中的方差； diffusion_coeff 表示公式 $(1)$ 中的 diffusion coefficient

# modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=LZC7wrOvxLdL
def marginal_prob_std(t, beta):
  # 参考公式 7
  return paddle.sqrt((beta**(2 * t) - 1.) / 2. / paddle.log(beta))

def diffusion_coeff(t, beta):
  # 参考公式 6 与公式 1
  return beta**t

beta =  paddle.to_tensor(25.)   # 该参数对应 ppdiffusors sde 中的 sigma
marginal_prob_std_fn = functools.partial(marginal_prob_std, beta=beta)
diffusion_coeff_fn = functools.partial(diffusion_coeff, beta=beta)

其中 Diffusion SDE 作者令 $\lambda(t) \propto 1 / \mathbb{E}\left[\left\|\nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))\right\|_2^2\right]$ 是为了使得 loss 在不同的时间步 $t$ 下保持平衡。

在确定好 loss function 之后，我们定义一个模型 ScoreNet （即前面公式中提到的 $s_\theta(\mathbf{x}, t)$）来对 score function 进行拟合。模型架构我们参考宋飏大佬在 Tutorial on Score-Based Generative Modeling 教程中的模型进行设计，具体模型架构可在 model.py 中查看。

对于模型架构，一个有意思的点是，论文中实用了 U-Net，并针对 U-Net 的结果除以 $\sigma$ 进行了归一化，原作者表示：

model output rescale by $1/\sqrt{\mathbb{E}[\|\nabla_{\mathbf{x}}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0)) \|_2^2]}$）， this rescaling helps capture the norm of the true score。

笔者理解大概意思可能为：由于我们实用 $s_\theta(\mathbf{x}, t)$ 拟合 $\nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))$，其中 $\nabla_{\mathbf{x}(t)}\log p_{0t}(\mathbf{x}(t) \mid \mathbf{x}(0))$ 的方差为 $\frac 1{\sigma^2}$。因此优化后的 $s_\theta(\mathbf{x}, t)$ 也会有同样的方差为 $\frac 1{\sigma^2}$，在 U-Net 输出处除以 $\sigma$ 能够使模型的输出方差保持在 1？从而使得模型训练更佳稳定？

3. 实践 - 模型训练

在确定好 loss 之后，可以使用 U-Net 进行训练，拟合 score function。 我们使用 MNIST 手写数字图片进行实现：

from paddle.vision.datasets import MNIST
from paddle.io import DataLoader
from paddle.vision.transforms import Compose, Normalize

batch_size = 128

transform = Compose([Normalize(mean=[0],std=[255])])
dataset = MNIST(mode='train', backend='cv2',transform=transform)
loader = DataLoader(dataset,
                    batch_size=batch_size,
                    shuffle=True,
                    num_workers=2)

Score Net 详细

import paddle.nn as nn
import paddle.nn.functional as F
import numpy as np
import paddle

# modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=LZC7wrOvxLdL
class GaussianFourierProjection(nn.Layer):
  """Gaussian random features for encoding time steps."""  
  def __init__(self, embed_dim, scale=30.):
    super().__init__()
    # Randomly sample weights during initialization. These weights are fixed 
    # during optimization and are not trainable.
    self.register_buffer("W", paddle.randn((embed_dim // 2,)) * scale)
  def forward(self, x):
    x_proj = x[:, None] * self.W[None, :] * 2 * np.pi
    return paddle.concat([paddle.sin(x_proj), paddle.cos(x_proj)], axis=-1)


class Dense(nn.Layer):
  """A fully connected layer that reshapes outputs to feature maps."""
  def __init__(self, input_dim, output_dim):
    super().__init__()
    self.dense = nn.Linear(input_dim, output_dim)
  def forward(self, x):
    return self.dense(x)[..., None, None]


class ScoreNet(nn.Layer):
  """A time-dependent score-based model built upon U-Net architecture."""

  def __init__(self, marginal_prob_std, channels=[32, 64, 128, 256], embed_dim=256):
    """Initialize a time-dependent score-based network.

    Args:
      marginal_prob_std: A function that takes time t and gives the standard
        deviation of the perturbation kernel p_{0t}(x(t) | x(0)).
      channels: The number of channels for feature maps of each resolution.
      embed_dim: The dimensionality of Gaussian random feature embeddings.
    """
    super().__init__()
    # Gaussian random feature embedding layer for time
    self.embed = nn.Sequential(GaussianFourierProjection(embed_dim=embed_dim),
         nn.Linear(embed_dim, embed_dim))
    # Encoding layers where the resolution decreases
    self.conv1 = nn.Conv2D(1, channels[0], 3, stride=1, bias_attr=False)
    self.dense1 = Dense(embed_dim, channels[0])
    self.gnorm1 = nn.GroupNorm(4, num_channels=channels[0])
    self.conv2 = nn.Conv2D(channels[0], channels[1], 3, stride=2, bias_attr=False)
    self.dense2 = Dense(embed_dim, channels[1])
    self.gnorm2 = nn.GroupNorm(32, num_channels=channels[1])
    self.conv3 = nn.Conv2D(channels[1], channels[2], 3, stride=2, bias_attr=False)
    self.dense3 = Dense(embed_dim, channels[2])
    self.gnorm3 = nn.GroupNorm(32, num_channels=channels[2])
    self.conv4 = nn.Conv2D(channels[2], channels[3], 3, stride=2, bias_attr=False)
    self.dense4 = Dense(embed_dim, channels[3])
    self.gnorm4 = nn.GroupNorm(32, num_channels=channels[3])    

    # Decoding layers where the resolution increases
    self.tconv4 = nn.Conv2DTranspose(channels[3], channels[2], 3, stride=2, bias_attr=False)
    self.dense5 = Dense(embed_dim, channels[2])
    self.tgnorm4 = nn.GroupNorm(32, num_channels=channels[2])
    self.tconv3 = nn.Conv2DTranspose(channels[2] + channels[2], channels[1], 3, stride=2, bias_attr=False, output_padding=1)    
    self.dense6 = Dense(embed_dim, channels[1])
    self.tgnorm3 = nn.GroupNorm(32, num_channels=channels[1])
    self.tconv2 = nn.Conv2DTranspose(channels[1] + channels[1], channels[0], 3, stride=2, bias_attr=False, output_padding=1)    
    self.dense7 = Dense(embed_dim, channels[0])
    self.tgnorm2 = nn.GroupNorm(32, num_channels=channels[0])
    self.tconv1 = nn.Conv2DTranspose(channels[0] + channels[0], 1, 3, stride=1)
    
    # The swish activation function
    self.act = lambda x: x * F.sigmoid(x)
    self.marginal_prob_std = marginal_prob_std
  
  def forward(self, x, t): 
    # Obtain the Gaussian random feature embedding for t   
    embed = self.act(self.embed(t))    
    # Encoding path
    h1 = self.conv1(x)    
    ## Incorporate information from t
    h1 += self.dense1(embed)
    ## Group normalization
    h1 = self.gnorm1(h1)
    h1 = self.act(h1)
    h2 = self.conv2(h1)
    h2 += self.dense2(embed)
    h2 = self.gnorm2(h2)
    h2 = self.act(h2)
    h3 = self.conv3(h2)
    h3 += self.dense3(embed)
    h3 = self.gnorm3(h3)
    h3 = self.act(h3)
    h4 = self.conv4(h3)
    h4 += self.dense4(embed)
    h4 = self.gnorm4(h4)
    h4 = self.act(h4)

    # Decoding path
    h = self.tconv4(h4)
    ## Skip connection from the encoding path
    h += self.dense5(embed)
    h = self.tgnorm4(h)
    h = self.act(h)
    h = self.tconv3(paddle.concat([h, h3], axis=1))
    h += self.dense6(embed)
    h = self.tgnorm3(h)
    h = self.act(h)
    h = self.tconv2(paddle.concat([h, h2], axis=1))
    h += self.dense7(embed)
    h = self.tgnorm2(h)
    h = self.act(h)
    h = self.tconv1(paddle.concat([h, h1], axis=1))

    # Normalize output
    h = h / self.marginal_prob_std(t)[:, None, None, None]
    return h

相关信息

在训练过程中，我们对公式 $(5)$ 定义的 loss 进行优化，执行以下代码，训练结束后，大致的 LOSS 会在 17 左右。

如果执行时，出现 tqdm.notebook 不存在等错误，可尝试升级 tqdm 版本。

若问题仍无法解决，请尝试移除 processor 相关代码后再执行。

模型训练：

# modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=LZC7wrOvxLdL
from paddle import nn
n_epochs = 50
learning_rate = 1e-4

model = ScoreNet(marginal_prob_std_fn)

optimizer = paddle.optimizer.AdamW(learning_rate=learning_rate,
                          parameters=model.parameters())

try:
    from tqdm.notebook import trange
    processor = trange(n_epochs * len(loader))
except:
    raise RuntimeError("Please upgrade tqdm to enable progress bar.")

for epoch in range(n_epochs):
    avg_loss = 0.
    num_items = 0.
    for x, y in loader:    
        optimizer.clear_grad()
        loss = loss_fn(model, x, marginal_prob_std_fn) 
        loss.backward()    
        optimizer.step()
        avg_loss += loss.item() * x.shape[0]
        num_items += x.shape[0]

        # tqdm 有问题时，移除下面两行代码
        processor.update()
        processor.set_description(f"Current Loss: {avg_loss / num_items:5f}")
    layer_state_dict = model.state_dict()
    paddle.save(layer_state_dict, f"model.pdparams")

4. 实践 - 反向过程及采样

4.1 Sampling with Numerical SDE Solvers

由于我们在前项传导（公式 $6$）中，假定了：

$$\begin{aligned} d \mathbf{x} = \beta^t d\mathbf{w}, \quad t\in[0,1] \end{aligned}\tag9$$

并且有 $s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}(t)} \log p_t(\mathbf{x}(t))$ 。根据公式 $(2)$ ，可以得到反向过程为：

$$\begin{aligned} d\mathbf{x} &=[\mathbf{f}(\mathbf{x}, t) - g^2(t)\nabla_{\mathbf{x}}\log p_t(\mathbf{x})] dt + g(t) d\bar{\mathbf{w}}\\ &= -\beta^{2t} \nabla_\mathbf{x} \log p_t(\mathbf{x}) dt + \beta^t d \bar{\mathbf{w}} \\ &\approx -\beta^{2t} s_\theta(\mathbf{x}, t) dt + \beta^t d \bar{\mathbf{w}} \end{aligned}\tag{10}$$

有了反向过程，我们还需要一个初始值 $x_0$ 进行采样。我们可以从公式 $(8)$ 的分布 $\mathbf{N}\bigg(\mathbf{x}; \mathbf{0}, \frac{1}{2 \log \beta}(\beta^2 - 1)\mathbf{I}\bigg)$ 中采样出 $x_0$；

很关键的一步，我们可以通过数学推导的方式来求得具体的反向过程。比如可以参考 Euler-Maruyama 方案，该方案将 $dt$ 替换为 $\Delta t$ ，$d \mathbf{w}$ 替换为 $\mathbf{z} \sim \mathcal{N}(\mathbf{0}, g^2(t) \Delta t \mathbf{I})$ 来实现对公式 $(10)$ 的离散化。于是，具体的采样过程就是：

$$\begin{aligned} \mathbf{x}_{t-\Delta t} = \mathbf{x}_t + \beta^{2t} s_\theta(\mathbf{x}_t, t)\Delta t + \beta^t\sqrt{\Delta t} \mathbf{z}_t, \end{aligned}\tag{11}$$

我们可以将以上过程通过代码实现：

# modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=LZC7wrOvxLdL
import tqdm
from PIL import Image

model = ScoreNet(marginal_prob_std_fn)
load_layer_state_dict = paddle.load("model.pdparams")
model.set_state_dict(load_layer_state_dict)

num_steps =  500
def Euler_Maruyama_sampler(score_model, 
                           marginal_prob_std,
                           diffusion_coeff, 
                           batch_size=32, 
                           num_steps=num_steps,  
                           eps=1e-3):
    """Generate samples from score-based models with the Euler-Maruyama solver.

    Args:
        score_model: s_\theta(x,t)
        marginal_prob_std: A function that gives the standard deviation of
        the perturbation kernel.
        diffusion_coeff: The \beta. A function that gives the diffusion coefficient of the SDE.
        eps: The smallest time step for numerical stability.
    
    Returns:
        Samples.    
    """
    t = paddle.ones((batch_size,))
    
    # 采样 x_0
    init_x = paddle.randn((batch_size, 1, 28,28)) \
    * marginal_prob_std(t)[:, None, None, None]
    
    # eps 试试调整以下 eps，看下生成的图片有什么变化
    time_steps = paddle.linspace(1., eps, num_steps)
    step_size = time_steps[0] - time_steps[1]
    x = init_x
    try:
        tqdm_processor = tqdm.notebook.tqdm
    except:
        tqdm_processor = tqdm.tqdm
    with paddle.no_grad():
        for time_step in tqdm_processor(time_steps):    
            batch_time_step = paddle.ones((batch_size,)) * time_step
            g = diffusion_coeff(batch_time_step)
            mean_x = x + (g**2)[:, None, None, None] * score_model(x, batch_time_step) * step_size
            x = mean_x + paddle.sqrt(step_size) * g[:, None, None, None] * paddle.randn(x.shape)      
    # 在最后一步中，我们不添加任何噪声
    return mean_x

def display_images(sample_img):
    if len(sample_img.shape) == 3:
        sample_img = sample_img[None,:,:,:]
    # sample_img = sample_img.squeeze(1)
    images = sample_img.clip(0,1).transpose([0,2,3,1]).numpy()
    images = images[:,:,:,0]
    images = (images * 255).round().astype("uint8")
    pil_images = [Image.fromarray(image) for image in images]
    for image in pil_images:
        image.show()

sample_img = Euler_Maruyama_sampler(model, 
                           marginal_prob_std_fn,
                           diffusion_coeff_fn, 
                           batch_size=4, 
                           num_steps=num_steps,  
                           eps=1e-3)
display_images(sample_img)

image-20230911233236881

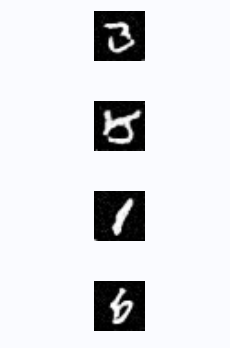
5. 小结 - SDE 基础概念

至此，我们了解了 Diffusion SDE 的大致流程，包括 diffusion 的 forward 和 backward 两个过程。以及如何通过 score match 的优化目标来训练 score function。

1. 我们将 diffusion 与 SDE 建立了联系，并使用 SDE 作为 diffusion 前项过程。
2. 我们通过 score matching 确定了 loss function，并使用 UNet 拟合了 score funciton，即 $s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}(t)} \log p_t(\mathbf{x}(t))$
3. 根据这个 SDE 前项过程，我们通过数学推导的方式 ( Euler-Maruyama)，确定了反向推导的流程。并使用训练好的 UNet 进行了采样，采样的结果如上所示，能明显看出采样生成的手写数字，效果是很不错的。

6. 理论 - Score-based generative models

我们在上文中，大致介绍了 Diffusion SDE 模型的 pipeline。在下文中，我们来欣赏 Diffusion SDE 背后的思想。我们需要了解 score function，Langevin Dynamics 和 MCMC。

6.1 Score Function

搭建一个生成模型时，通常会考虑得到他的概率分布 $P(x)$，如果我们选择模型作为该生成模型的概率分布：

$$q_\theta(x) = \frac {e^{-f_\theta(x)}}{Z_\theta} \tag{12}$$

其中 $Z_\theta$ 为配分参数，用于标准化 。而 $f_\theta(x)$ 通常称为能量分布（energy-based model）（似乎上面这种分布再物理中很常见）。为了求得 $q_\theta(x)$，通常我们会最大化他的对数似然函数

$$L_\theta=\mathbb{E}_{x \sim p(x)}\left[-\log q_\theta(x)\right] \tag{13}$$

然后得到 $q_\theta(x)$ 之后进行采样。但 $q_\theta(x)$ 中存在难以计算的 $Z_\theta$ ，为避免 $Z_\theta$ ，我们可以考虑对 score function 下手，一个分布 $\mathrm{p}(x)$ 的 score function 定义为 the gradient of log-density，即：

$$\nabla_{\mathrm{x}} \log \mathrm{p}(\mathrm{x})\tag{14}$$

如果我们求得 score function：

$$\begin{aligned} s_\theta(x) &\approx \nabla_{\mathrm{x}} \log \mathrm{q}(\mathrm{x})\\ &= -\nabla_{\mathrm{x}} f_\theta(x) - \nabla_{\mathrm{x}} \log Z_\theta \\ &= -\nabla_{\mathrm{x}} f_\theta(x) \end{aligned}\tag{15}$$

那么，我们就可以使用 Langevin dynamics 来进行采样。

6.2 Langevin Dynamics 和 MCMC

Metropolis-adjusted Langevin algorithm (MALA) 或 Langevin Monte Carlo (LMC) 是一种通过 MCMC 来从难以直接计算的分布中采样的方法。MCMC 为 Markov Chain Monte Carlo，采样的过程可以视为不同 state 之间的随机游走转换，其中初始化值从 $\pi(x)$ 中采样，采样的过程可表示为以下公式：

$$x_{t+1}=x_t- \varepsilon \nabla_{\mathbf{x}} \log p(x_t)+\sqrt{2\varepsilon} \alpha, \quad \alpha \sim \mathcal{N}( 0,1)\tag{16}$$

当 $\epsilon \rightarrow 0, t \rightarrow \infty$ 时，通过上述分布采样出来的 $x_K$ 会服从于 $P(x)$ ，或者可以说，上式会收敛于 $P(x)$。因此，我们只需要对图像分布 $P(x)$ 的 score function $s_\theta(x) \approx \nabla_{\mathrm{x}} \log \mathrm{q}(\mathrm{x})$ 进行公式 $(16)$ 的迭代，那么我们相当于从图像分布 $P(x)$ 进行采样。Langevin Dynamics 和 MCMC 更多参考：网友博客 - MCMC

6.3 Score Matching

以上介绍了求得 score funciton $s_\theta(x) \approx \nabla_{\mathrm{x}} \log \mathrm{q}(\mathrm{x})$ 之后，我们能够通过 Langevin dynamic 进行采样。

以下为求解 score funciton 的方法做简单介绍。为了求得 score function，我们可以优化 Fisher Divergence：

$$\mathbb{E}_{x\sim p(x)}\left[\left\|\nabla_x \log p(x)-s_\theta(x)\right\|_2^2\right]\tag{17}$$

可以通过 [Score Matching](Estimation of Non-Normalized Statistical Models by Score Matching) 的方式优化上面这个式子。关于 score matching，这部分较为复杂，如果对其背后原理感兴趣的读者，可以参考:

1. Estimation of non-normalized statistical models by score matching
2. A connection between score matching and denoising autoencoders
3. Sliced score matching: A scalable approach to density and score estimation

6.4 Sampling with Predictor-Corrector Methods

参考以上结论，所以我们不需要知道 $\nabla_{\mathbf{x}} \log p(x)$ 便能对 score function 进行优化了，求得 $s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}(t)} \log p_t(\mathbf{x}(t))$，这个模型也可以称为 score-based model。假设我们采样得到了 $x_0$，那么我们可以通过 Langevin Dynamics 和 MCMC （公式 $(16)$）来进行采样。

Predictor-Corrector samplers 结合了 numerical SDE solvers （参考上一章节中我们使用的采样器）和 Langevin MCMC。

1. 对于 predictor step：我们使用 numerical SDE solvers 来根据 $x_t$ 采样 $x_{t-\Delta t}$。
2. 对于 corrector step：我们使用 Langevin MCMC 来修正 $x_t$，这样我们的预测 $x_t$ 会更准确。

# Modified from https://colab.research.google.com/drive/120kYYBOVa1i0TD85RjlEkFjaWDxSFUx3?usp=sharing#scrollTo=zOsoqPdXHuL5

import numpy as np

signal_to_noise_ratio = 0.2
num_steps =  500

def pc_sampler(score_model, 
               marginal_prob_std,
               diffusion_coeff,
               batch_size=64, 
               num_steps=num_steps, 
               snr=signal_to_noise_ratio,                
               eps=1e-3):
    """Generate samples from score-based models with Predictor-Corrector method.

    Args:
        score_model: A PyTorch model that represents the time-dependent score-based model.
        marginal_prob_std: A function that gives the standard deviation
        of the perturbation kernel.
        diffusion_coeff: A function that gives the diffusion coefficient 
        of the SDE.
        batch_size: The number of samplers to generate by calling this function once.
        num_steps: The number of sampling steps. 
        Equivalent to the number of discretized time steps.    
        device: 'cuda' for running on GPUs, and 'cpu' for running on CPUs.
        eps: The smallest time step for numerical stability.
    
    Returns: 
        Samples.
    """
    t = paddle.ones((batch_size,))
    init_x = paddle.randn((batch_size, 1, 28, 28)) * marginal_prob_std(t)[:, None, None, None]
    time_steps = np.linspace(1., eps, num_steps)
    step_size = time_steps[0] - time_steps[1]
    x = init_x
    try:
        tqdm_processor = tqdm.notebook.tqdm
    except:
        tqdm_processor = tqdm.tqdm
    with paddle.no_grad():
        for time_step in tqdm_processor(time_steps):      
            batch_time_step = paddle.ones((batch_size,)) * time_step
            # Corrector step (Langevin MCMC)
            grad = score_model(x, batch_time_step)
            grad_norm = paddle.norm(grad.reshape((grad.shape[0], -1)), axis=-1).mean()
            noise_norm = np.sqrt(np.prod(x.shape[1:]))
            langevin_step_size = 2 * (snr * noise_norm / grad_norm)**2
            x = x + langevin_step_size * grad + paddle.sqrt(2 * langevin_step_size) * paddle.randn(x.shape)      

        # Predictor step (Euler-Maruyama)
        g = diffusion_coeff(batch_time_step)
        x_mean = x + (g**2)[:, None, None, None] * score_model(x, batch_time_step) * step_size
        x = x_mean + paddle.sqrt(g**2 * step_size)[:, None, None, None] * paddle.randn(x.shape)      
    
    # 在最后一步中，我们不添加任何噪声
    return x_mean

sample_img = pc_sampler(model, 
               marginal_prob_std_fn,
               diffusion_coeff_fn,
               batch_size=4, 
               num_steps=num_steps, 
               snr=signal_to_noise_ratio,                
               eps=1e-3)
display_images(sample_img)

image-20230911233304453

$$\begin{aligned} L = &\mathbb{E}_{x\sim p(x)}\left[\left\|\nabla_x \log p(x)-s_\theta(x)\right\|_2^2\right]\\ =& \int p(\mathbf{x})\left[\left\|\mathbf{s}_\theta(\mathbf{x})\right\|^2- 2tr\nabla_x s_{\theta}(x) \right] d \mathbf{x} + const \end{aligned}\tag{18}$$

总结

本文基于宋飏大佬的博客及 torch 的 Colab 教程做了笔记整理。初步探讨了论文 SCORE-BASED GENERATIVE MODELING THROUGH STOCHASTIC DIFFERENTIAL EQUATIONS 中 SDE 模型的大致思想。