skip-gram 的优化（细节熟记）

介绍“Distributed Representations of Words and Phrases and their Compositionality“ 一文中提出的三种方案：Subsampling, Negative sampling 与 Hierarchical Softmax

大部分的笔记参考了 peghoty 的博客 word2vec 中的数学

$$\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log P\left(w_{t+j} \mid w_{t}\right)$$

优化的背景是大家熟悉的一个问题：skip-gram 每次梯度优化 softmax 时候，时间复杂度 O(M) 太高。

相关图片

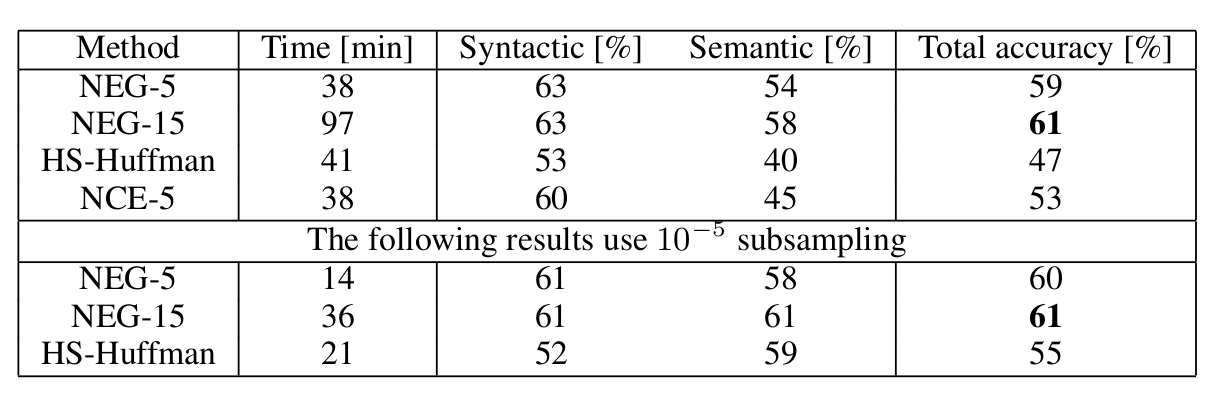
从上表可以看出 NEG 的效率的确有点高，是一个应该好好掌握的技术。。

Sub-sampling

为了解决单词分布不平衡的问题，每个词在训练时都有 $P(w_i)=1-\sqrt{\frac t{f(w_i)}}$ 的概率被丢弃（不训练）。$f(w_i)$ 是单词出现的频率，$t$ 是一个闸值，通常为$10^{-5}$。

Negative sampling

将 softmax 替换为二分类问题。对单词 w 的每个正样本，我们选取 k 个副样本进行二分类。使正样本的概率最大化，负样本概率最小化。

即对于每个中心词 w 我们最大化：

$$g(w)=\prod_{\widetilde{w} \in \operatorname{Context}(w)} \prod_{u \in\{w\} \cup N E G^{\tilde{w}}(w)} p(u \mid \widetilde{w})$$

求对数似然：

$$\begin{aligned} \mathcal{L}=& \log G=\log \prod_{w \in \mathcal{C}} g(w)=\sum_{w \in \mathcal{C}} \log g(w) \\ =& \sum_{w \in \mathcal{C}} \log \prod_{\widetilde{w} \in \text { Context }(w)} \prod_{u \in\{w\} \cup N E G^{\tilde{w}}(w)}\left\{\left[\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right]^{L^{w}(u)} \cdot\left[1-\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right]^{1-L^{w}(u)}\right\} \\ =& \sum_{w \in \mathcal{C}} \sum_{\widetilde{w} \in \operatorname{Context}(w)} \sum_{u \in\{w\} \cup N E G \tilde{w}(w)} \\ &\left\{L^{w}(u) \cdot \log \left[\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right]+\left[1-L^{w}(u)\right] \cdot \log \left[1-\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right]\right\} \end{aligned}$$

通过梯度求参数的更新公式：

$$\theta^{u}:=\theta^{u}+\eta\left[L^{w}(u)-\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right] \mathbf{v}(\widetilde{w})\\ \frac{\partial \mathcal{L}(w, \widetilde{w}, u)}{\partial \mathbf{v}(\widetilde{w})}=\left[L^{w}(u)-\sigma\left(\mathbf{v}(\widetilde{w})^{\top} \theta^{u}\right)\right] \theta^{u}\\ \mathbf{v}(\widetilde{w}):=\mathbf{v}(\widetilde{w})+\eta \sum_{u \in\{w\} \cup N E G^{\tilde{w}}(w)} \frac{\partial \mathcal{L}(w, \widetilde{w}, u)}{\partial \mathbf{v}(\widetilde{w})}$$

有了梯度便可以优化了，总体算法伪代码如下：

相关图片

一些注意点

• 负样本小数据选 5-20，大数据 2-5

• 噪音（负样本）选取概率 $P\left(\omega_{i}\right)=\frac{f\left(\omega_{i}\right)^{3 / 4}}{\sum_{j=1}^{n} f\left(\omega_{j}\right)^{3 / 4}}$

• Noise Contrastive Estimation 与 NEG 的区别：

  • NCE 需要考虑对应负样本以及噪声出现的概率

• 负采样对高频词和低纬度向量表现好（作者用的 300），hierachical 对低频词往往表现的更好

Hierarchical Softmax

用二叉树作为解码层，每个 leave 一个单词。每个节点有参数$\theta$，通过 sigmoid 进行二分类判断节点往左走还是右走。

使用 haffman 树性能更好，性能更高，具体使用什么树性能有很多差别。下面为使用 Haffman 的 HIerarchical softmax

定义：

相关图片

给定 context，选中正确中心词 $w$ 的概率为：

$$p(w \mid \operatorname{Context}(w))=\prod_{j=2}^{l^{w}} p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)$$

其中

$$p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left\{\begin{array}{ll} \sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right), & d_{j}^{w}=0 \\ 1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right), & d_{j}^{w}=1 \end{array}\right.$$

$$p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d_{j}^{w}}$$

我们可以确保所有叶子上词相加后总概率为 1，只要我们确保每个节点下两个分支概率相加为 1。

然后极大对数似然函数：

$$\begin{aligned} \mathcal{L} &=\sum_{w \in \mathcal{C}} \log \prod_{j=2}\left\{\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d_{j}^{w}}\right\} \\ &=\sum_{w \in \mathcal{C}} \sum_{j=2}^{l^{w}}\left\{\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]\right\} \end{aligned}$$

然后通过随即梯度上升法优化。其中我们有两种参数需要优化：

• hidden layer 与 input layer 间的权重参数$v$。
• hidden layer 之后的权重参数（也就是树上的权重$\theta$）

$$\theta_{j-1}^{w}:=\theta_{j-1}^{w}+\eta\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w}$$

（梯度更新）

伪代码方便理解

相关图片

注意点：

• 每个节点计算完之后，都会进行一次对应的 $\theta$ 优化。
• 在每个词 u 计算后都会进行一次 v 的优化。（word2vec 源码的操作，似乎效果更好）
• v 的更新量在 $\theta$ 更新前记录好

特点：

• 一共执行平均 log（M）次 sigmoid 以及$\theta^TX$
• 缺点：找到生僻词会相对耗时久

细节

Sigmoid

背景：计算机的指数运算通常都是利用幂级数展开求，较为费时。

计算时将 sigmoid 近似为：

$$\sigma(x) \approx\left\{\begin{array}{ll} 0, & x \leq-6 \\ \sigma\left(x_{k}\right), & x \in(-6,6) \\ 1, & x \geq 6 \end{array}\right.$$

其中，我们对 （-6，6）区间进行划分，并计算每个区域对应的 sigmoid 值。通过查表来计算 sigmoid 的近似值，以提升运算效率。

词典检索优化

通过哈希表提高词典检索效率

开设长为 vocab_hash_size 的整形数组 vocab_hash 并初始化为 -1.

令 vocab_hash[hv(w[j])] = j, hv(w[j])表示第 j 个词的哈希值。

通过 open-address 解决哈希值冲突问题，当冲突时检索哈希表中下一个槽。

查找某个单词 u 时，计算 vocab_hash[hv(u)]，若为-1 则为为收入。否则检验 u ?= w[vocab_hash[hv(u)]]，若相同则匹配，否则向下继续查找。

低频词和高频词处理

通常根据当前字典的规模决定是否进行低频词清理，如当 $|D_{current}|>0.7\times \text{vocab hash size}$，则进行低频词处理，通常阀值为 5。

如 sub-sampling 中提到的，对于高频词，我们有一定的几率舍弃它，而 word2vec 源码中使用的丢弃概率公式为：

$$\operatorname{prob}(w)=1-\left(\sqrt{\frac{t}{f(w)}}+\frac{t}{f(w)}\right)$$

窗口及上下文

训练样本过大，模型训练以行为单位进行以确保内存安全。或者可以设置 MAX_SENTENCE_LENGTH 。

学习率

word2vec 中的初始为 0.025。学习率根据以处理词数调整。

$$\eta=\eta_{0}\left(1-\frac{\text { word count actual }}{\text { train words }+1}\right)$$

参数初始化

word2vec 的初始化函数，其中 m 为单词长度。

$$\frac{[\text { rand }() / \text { RAND MAX }]-0.5}{m}$$

多线程并行

word2vec 中对于多线程的实现

相关图片