开篇：关于这本书和算法

（我）阅读次书主要为了理解计算机程序实现算法整个过程，一个只能表示 0 和 1 的机器，是如何高效的进行一系列运算，最后得到我们所提问题的结果。算法优化不仅应该停留在数学层面上的优化，也应该针对算法实现的过程进行优化。而今科技日新月异，传统计算机被摩尔定律等条件限制了发展的速度，希望能从本书中获得一些启发来把握新科技技术的优势（如量子计算机）使算法能够以最高效的方式运行。

这系列博客将用来记录我阅读中遇到的重点信息，个人笔记，或者有趣的题目:) 。你可以通过标签 TAOCP 或 计算机程序艺术 找到他们。对于本书中那些参考答案奇怪的题目，我会尽力给出详细合理的答案。

本文参考《计算机程序艺术》第 3 版 国防工业出版社 及《Knuth D. - The art of computer programming. Volume 1-AW (1968) 》，对于中文版书籍与英文原著表达不一处，均已原著为准。

公式很多，预期加载时间 1 分钟。

特别的阅读流程

没有什么比具有逻辑思维的前言更能吸引一位热爱计算机程序的读者，以下是这本书前言中的一份阅读流程建议。看完这部分后我竟然有种想要通宵好几天一口气读完它的冲动！

计算机程序设计艺术第一卷高清中文版

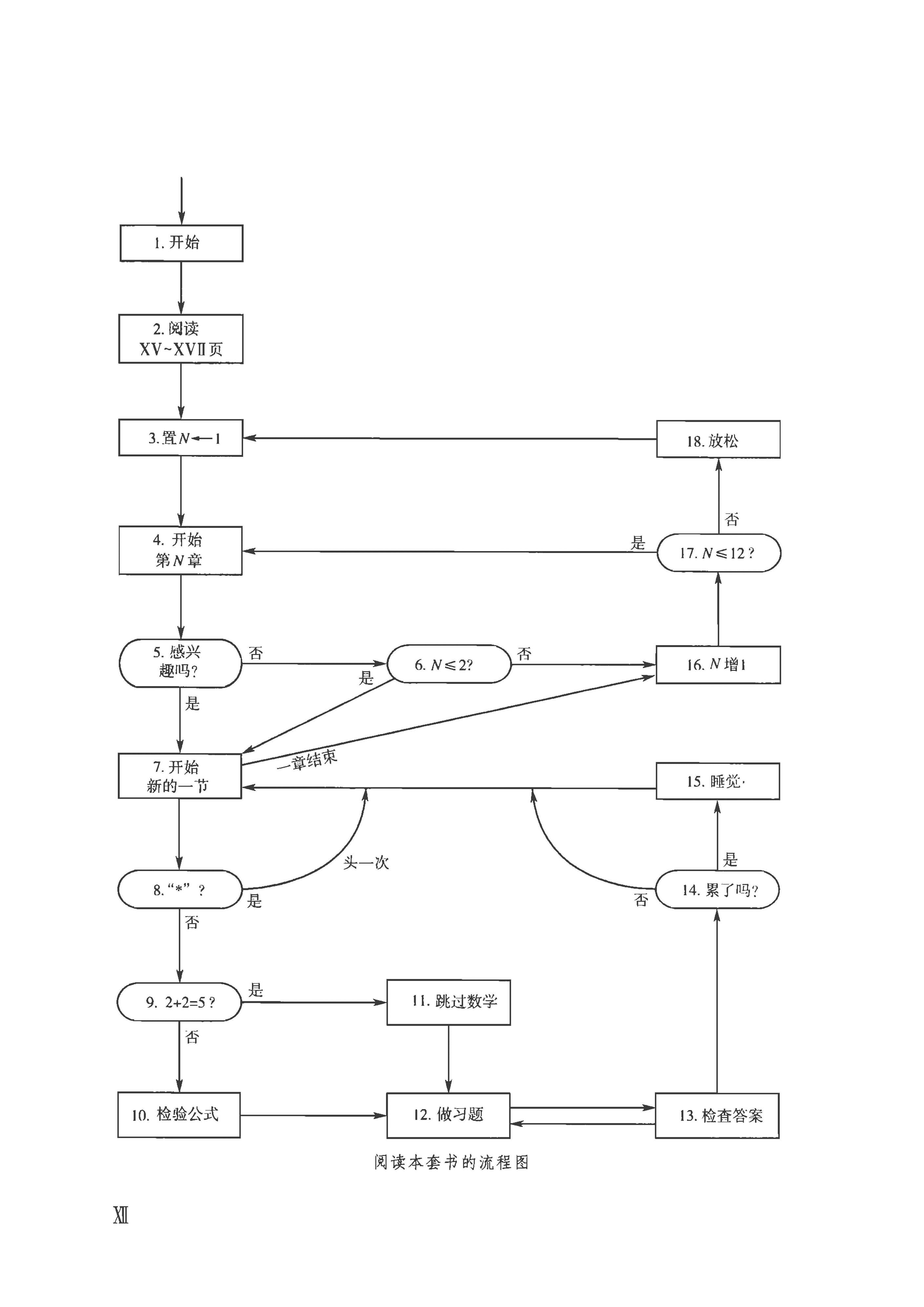
然后我就随手写了一下代码，用来加深对阅读流程的理解哈。

N = 1
while N <= 12:
    章 = N
    if 对本章感兴趣:
        for 节 in 章:
            if 第一次阅读本节且本节以*开头:
                你可以选择 continue
            if 你爱数学:
                校验这一节中的数学推导，并把错误告诉作者
                for 习题 in 关于习题的说明中给出的提示做本节的练习题:
                    做
                    对答案 if 有答案
                if 累了:
                    睡觉
                    break
            else:
                如果这一章充满了数学推导，你最好略去不读。但你应该熟悉这一节的基本结果。
                这些基本结果通常在开始处附近叙述，或者在困难部分的末尾用斜体字叙述
    else:
        if N <= 2:
            本章挺重要，还是大致看一看
        else:
            N += 1
            if N in (3,5,7,9,11):
                进入下一卷
恭喜你，来说服你的朋友购买第 1 卷，并开始阅读他吧

习题分数

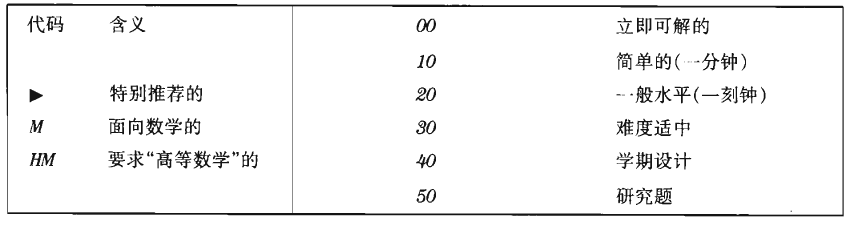
书中习题会有对应的分数来提示读者该题的难度，我也会在文中附上这些信息，具体如下：

分数：解释 00：一个极其容易的问题,如果你已理解正文的内容,就可能立即做出回答。 这样一道题几乎总是可以“眉头一披”就把它做出。 10：一个简单的问题。它要求你去思考刚刚学过的内容,但绝不意味着是困 难的。你应当有能力在顶多一分钟之内就把它做出。在获得解答的过程 中可能要用到笔和纸。 20：一个普通的问题。它检查你对正文内容的基本理解,但你可能需要 十五 或二十分钟 才能完整地回答它。 30：一个中等难度或中等复杂的问题。这个题目可能需要 两个小时 以上的 工作才能令人满意地解决。或者甚至更长时间,如果电视机开着的 话。 40：确实是一个十分困难或咒长的问题。在学校里, 它将适合于作为一个学 期的课程设计。一个学生应当有能力在相当长的时间里来解决它,但这 个解不会是平凡的。 50：就作者在编写本书时所知,这是一个还未令人满意地解决的问题,尽管已 经有很多人做了尝试。如果你已经找到了这样- -个问题的答案,你应当把他发表出来

image-20201215112933020

第一章 基本概念

1.1 程序和算法

• 算法的定义

《Knuth D. - The art of computer programming. Volume 1-AW (1968) 》将算法定义为一个四元组 $\{(Q,I,\Omega,f)\}$，四个变量分别表示计算状态，输入，输出及计算规则。其中，$Q$包含 $I$和$\Omega$，$f$是从$Q$到自身的一个函数， $\forall q \in \Omega, f(q) = q$，（因为$\Omega$为输出集）。

集合 $I$ 中的每一个输入 $x$ 定义一个计算序列 $x_{0}, x_{1},$ $x_{2}, \cdots$ 如下 :

$$x_{0}=x \quad \text { and } \quad \text { for } k \geqslant 0, \quad x_{k+1}=f\left(x_{k}\right)$$

如果 $k$ 是使 $x_{k}$ 在 $\Omega$ 中的最小的整数，就说计算序列在 $k$ 步中终止，而且在此种情况下，说从 $x$ 产生出输出 $x_{k}$。 (注意,如果 $x_{k}$ 在 $\Omega$ 中,则 $x_{k+1}$ 也是。因为在这样的情况下，$x_{k+1}=x_{k}$。 某些计算序列可能永不终止；一个算法是对于 $I$ 中所有的 $x$ 在有限多步中终 止的计算方法。

• 算法的能行性

能行的算法（或称有效的算法）是指它的所有运算必须是充分基本的，在原则上人用笔和张都能在有限时间内精确的完成的。设计具有能行性的算法相当于对算法的概念加上限制，使得它仅涉及初等的运算。

习题参考

• 题 8. [M 25]算法的能行性

题：通过描述等式( 3$)$ 中的 $\theta_{j}, \phi_{j}, a_{j}, b_{j},$ 给出计算正整数 $m$ 和 $n$ 的最大公因子的一个 “能行的”形式算法。令输人由串 $a^{m} b^{n}$ 表示,即 $m$ 个 $a$ 后边跟着 $n$ 个 $b_{\circ}$

答：

$$\begin{aligned} &\text { 命 } A=\{a, b, c\}, N=5 \circ \text { 这个算法将以字符串 } a^{\operatorname{grd}(m, n)} \text { 结束. }\\ &\begin{array}{cccccl} j & \theta_{j} & \phi_{j} & b_{j} & a_{j} & \text { 备注}\\ 0 & a b & (\text { 空 }) & 1 & 2 & \text { 删掉一个 } a \text { 和一个 } b \text { ,若无 a 或 b 则转到 } 2 \\ 1 & (\text { 空 }) & c & 0 & 0 & \text { 把 } c \text { 加到左端,返回到 } 0 \\ 2 & a & b & 2 & 3 & \text { 把所有 } a \text { 变成 } b \\ 3 & c & a & 3 & 4 & \text { 把所有 } c \text { 变成 } a \\ 4 & b & b & 0 & 5 & \text { 如果还剩有 } b \text { ,则重复 } \end{array} \end{aligned}$$

具有能行性的算法可能可以很好的解释计算机程序如如何实现一个具体算法的，理解这点可以更好的根据计算机的某些特性来实现算法的优化。在答案中的标志分别表示， $j$ ：计算步骤 ，$\theta_{j}$ ：原串（string）， $\phi_{j}$ ：代替原串的串， $b_{j}$ ：如果有原串，那么运行第 $b_j$ 步骤， $ a_{j}$：如果没有原串，那么运行第 $a_j$ 步骤。如果理解了这些符号的含义，即使没有右边的备注，你也应该能够想象到整个算法的一笔一划是怎么实现的。

相关图片

• 题 9. ▲ [M 30] 理解程序 X 是算法 Y 的实现

题：假设程序 X 为 $C_1 = \{(Q_1,I_1,\Omega _1,f_1)\}$ ,算法 Y 为 $C_2 = \{(Q_2,I_2,\Omega _2,f_2)\}$，试表述 “$C_2$模拟$C_1$” 或 “$C_2$是$C_1$的表示”

答：我们可以说 $C_{2}$ 表示 $C_{1},$ 如果有从 $I_{1}$ 到 $I_{2}$ 的函数 $g$,从 $Q_{2}$ 到 $Q_{1}$ 的函数 $h,$ 和从 $Q_{2}$ 到正整数的函数 $j,$ 满足下列条件 :

a) 如果 $x$ 在 $I_{1}$ 中,则 $h(g(x))=x_{\text {. }}$

对于算法 Y 中的输入元素 $x$ ，$C_2$中的映射为$x_2 = g(x)$。那么有 $x_2$ 在$Q_1$中的映射为 $x$。即对于算法 Y 要求的每一个输入，计算机程序 X 总有一些状态来表示这个算法的输入。每一种计算机状态只能表示一个对应的算法输入。

b) 如果 $q$ 在 $Q_{2}$ 中,则 $f_{1}(h(q))=h\left(f_{2}^{[j(q)]}(q)\right),$ 其中 $f_{2}^{j(q)}$ 指的是函数 $f_{2}$ 被迭代 $j(q)$ 次。

为实现算法 Y 中的一个运算步骤 $f_1()$，计算机程序可能会迭代多次 $f_2()$。 如本节例题 8 中计算机通过一个循环来实现把所有的 c 替换成 a。

c) 如果 $q$ 在 $Q_{2}$ 中,则当且仅当 $q$ 在 $\Omega_{2}$ 中时 $h(q)$ 在 $\Omega_{1}$ 中。

计算机程序 X 中的输出状态只会对应到算法 Y 中的输出状态。

举个例子：

求最大公约数的欧几里得算法可以用这些术语表述如下 : 令 $C_{1}$ 中 $Q$ 为所有单点 $(n),$ 所有有序偶 $(m, n)$ 以及所有有序四元组 $(m, n, r, 1),(m, n, r, 2)$ 以及 $(m, n, p, 3)$ 的集合,其中 $m, n, p$ 是 正整数, $r$ 是一个非负整数。令 $I$ 是所有数偶 $(m, n)$ 的子集,并令 $\Omega$ 是所有单点 $(n)$ 的 子集。定义 $f$ 如下 :

$$\begin{aligned} &f((m, n))=(m, n, 0,1) ; \quad f((n))=(n) ;\\ &f((m, n, r, 1))=(m, n, m \text { 除以 } n \text { 的余数 } .2) ;\\ &f((m, n, r, 2))=(n), \text { 如果 } r=0, \quad \text { 否则 }(m, n, r, 3) ;\\ &f((m, n, p, 3))=(n, p, p, 1) \end{aligned}$$

那么对于模拟算法的计算机程序，令 $C_{2}$ 有 $I_{2}=\{(m, n)\}, \Omega_{2}=\{(m, n, d) |, Q_{2}=I_{2} \cup \Omega_{2} \cup$ $\{(m, n, a, b, 1)\} \cup${(m, n, a, b, 2)}\cup$\{(m, n, a, b, 3)\}\cup$ {(m, n, a, b, 4)}\cup $\{(m, n, a, b, 5)\}$

令

$$\begin{aligned} &f_{2}((m, n))=(m, n, n, n, 1) \\ &f_{2}((m, n, d))=(m, n, d) \\ &f_{2}((m, n, a, b,1 )=(m, n, a, b, a \bmod b, 2)\\ &\text{ 如果 }\ r=0, f_{2}((m, n, a, b, r, 2))=(m, n, b), \\ &\text{ 否则 }\ f_{2}((m, n, a, b,r, 2))=(m, n, a, b, r, 3) \\ &f_{2}((m, n, a, b, r, 3))=(m, n, b, b, r, 4) \\ &f_{2}((m, n, a, b, r, 4))=(m, n, a, r, 5) \\ &f_{2}((m, n, a, b, 5))=f_{2}((m, n, a, b, 1)) \end{aligned}$$

现在令

$$\begin{aligned} &h((m, n))=g(m, n)=(m, n) \\ &h((m, n, d))=(d)\\ &h((m, n, a, b, 1))=(a, b, 0,1)\\ &h((m, n, a, b, r, 2))=(a, b, r, 2) \\&h((m, n, a, b, r, 3))=(a, b, r, 3) \\ &h((m, n, a, b, r, 4))=h(f_{2}((m, n, a, b, r, 4))) \\ &h((m, n, a, b, 5))=(a, b, b, 1) \\ &j((m, n, a, b, r, 3))=j((m, n, a,b, r, 4))=2,\text{ 否则 }\ j(q)=1_{\circ} \end{aligned}$$

则 $C_{2}$ 表示 $C_{1}$

1.2 数学基础

1.2.1 数学归纳法

基础的归纳法大家应该都熟悉，文中总结了以下几个例子

扩充的欧几里得算法

image-20210105231410856

证明当每步执行 E2 时，$a^{\prime} m+b^{\prime} n=c, \quad a m+b n=d$ 总是成立。

假设第 k 次执行 E2 时等式成立，那么第 k+1 次执行 E2 时有：

$$\text{ 首先 }a_{k+1}m+b_{k+1}n = d_{k+1}\text{ 成立 },\text{ 前式成立 } ;\\ \text {然后证明后式: }\\ \because a^{\prime} m+b^{\prime} n=c, \quad a m+b n=d\\ \therefore (a_k' -qa_k)m + (b_k'-qb_k)n \\ =a_k'm-qa_km+b_k'n-qb_kn \\ =c_k-qd_k = r_{k}\\ \therefore am+b n=d \text{ 得证 }$$

除了归纳法证明，断言图使得我们对整个证明的逻辑过程，或者是程序的运转过程有了更深刻的理解。如下断言图，我们只要证明在给定先前状态$A_i$下，经过操作 $E_j$ 我们会进入状态 $A_{i+1}$。那么整个算法也就完成了证明。 归纳法或者断言法的关键在于，读者要以某些数据来运行算法一两遍，只有在脑袋中行成如下的断言，对每个计算机停留的状态和执行的处理了解，我们才算真正理解为什么一个算法是正确的。

image-20210105233507622

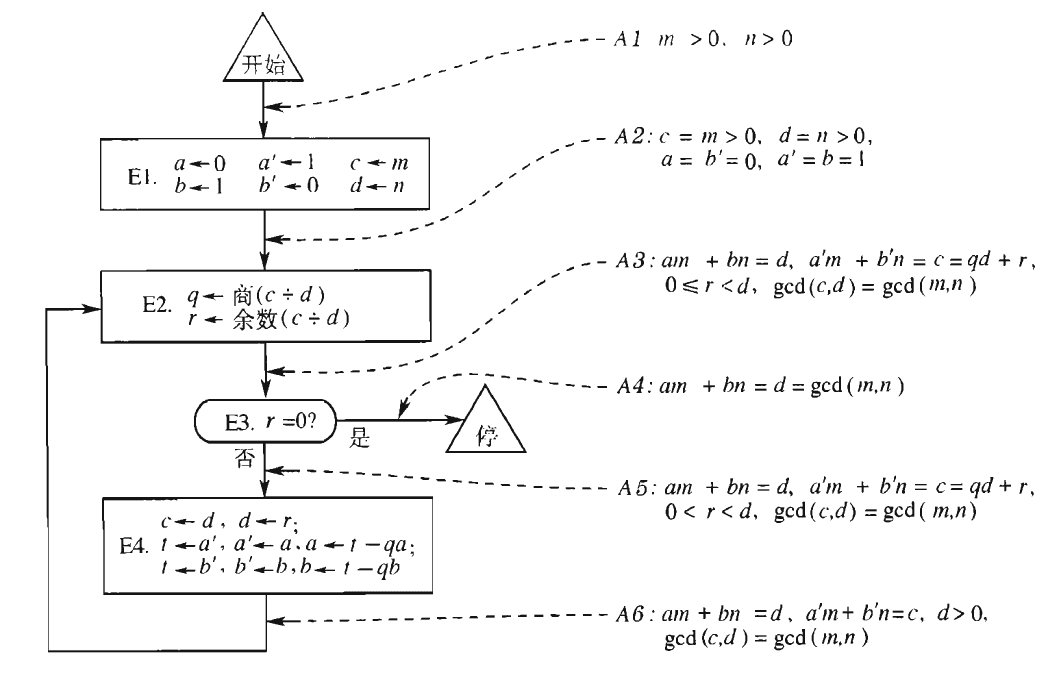
（图：欧几里得算法的断言图。来源：《计算机程序艺术 第一卷》p13）、

习题参考

• 习题 15. ▲ [HM 28]广义归纳法

正文中说明了怎样证明依赖于一个整数 n 的命题 P(n),但它没 有描述怎样证明依赖于两个整数的命题 P(m,n)。在这些情况下，通常是通过某种类型的“双重归纳法”来给出一个证明的，因而经常显得含糊不清。实际上，有一个比简单的归纳法更为一般的重要原理，它不仅适用于这种情况，而且还适用于关于不可数集合证明命题的情况一一例如， 对于所有实数 x 的 P(x)。这个一般原理叫做良序原理（well- ordering）

设“<”是集合 S 上的一个关系，它满足以下的性质 i)给定 S 中的 x,y 和 z,如果 x<y 和 y<z,则 x<z ii)给定 S 中的 x 和 y,以下三种可能性中恰有一种为真：x<y,x=y 或 y<x iii)如果 A 是 S 的任何非空子集，则 A 中有一个元素 x,使得对于 A 中所有的 y,有 x≤y(即或 x=y)

书中前三问太简单这里就略过了。

骗你是小狗

问： d)（字典序）设 S 对于<良序、而且对于 n>0 令$T_n$ 是 $S$ 中元素 $x$ 的所有 $n$ 元组$(x_1, x_2…x_n)$\text{ 的集合 }.\text{ 如果有某一个 }$k,1≤k≤n$,\text{ 使得在 }$S$\text{ 中 }.\text{ 对于 }$1≤j<k, x_j=y_j$,\text{ 但是 } x$x_k<y_k$ 则定义 $(x_1,x_2,...,x_n)<(y_1,y_2...,y_n)$。问 < 是否$T_n$的一个良序？

参考理解： 次初的 < 比较类似于两个有序的数列之间的对比，如 {1,2,3,4} < {1,3,2,4}, {1,7,8,9}<{4,1,2,3}。当 $n = 1$时，$T_n$ 为 $S$ 的非空子集，因此存在最小单位，条件 iii 得证。当 $n \ge 1$ 时，假设 $T_{n-1}$满足条件 iii，则 $T_{n-1}$的非空子集 $A_{x}$ 包含一个最小的元素。 $T_n$ 在 $T_{n-1}$ 的基础上添加一个分量， 因此$T_n$ 的非空子集也必定包含一个最小的元素。

问： f)试证<是 S 的一个良序当且仅当它满足上边的 i) 和 ii)，而且对于所有$j\ge 1$,不存在具有 $x_{j+1}<x_{j}$的无穷序列 $x1,x2,x3,...$。

参考理解： 如果条件一和二不满足，那么集合中两两之间的大小对比将陷入循环，若存在一直减小的无穷数列，那么这个集合也不存在最小的元素。应用到计算机算法中，如果我们能将计算机的每一个状态映射到良序集 S 中的每一个元素，并且使得 计算机的每次执行都能从一个状态 X 转到另一个状态 y，且满足 $F(y)<f(x)$，那么算法必然终止。

问： g)设 $S$ 对于 < 是良序，且设 $P(x)$ 是关于 S 的元素 x 的一个命题。试证如果在对于所有的 $y<x,P(y)$为真的假定下能证得 $P(x)$ 为真，则 $P(x)$对 $S$ 中的所有 $x$ 为真。

书中答案： g)令 $A$ 是使得 $P(x)$ 为假的所有的 x 的集合。如果 $A$ 非空，则它含有最小的元素 $x_0$。因此 $P(y)$ 对于所有 $y<x$ 为真。但这意味着 $P(x_0)$为真，所以 $x_0$不在 $A$ 中（矛盾）。因此 $A$ 必须为 空：即 $P(x)$ 总是为真。

参考理解： 根据本题下面的注解，以 S=正整数的情况为例，我们需证明对所有 $y<1$ ,如果 $P(y)$ 为真，则$P(1)$ 为真。然而因为 $P(y)$ 为空 ，所以我们变成了直接证明$P(1)$ 为真。上述就是我们原来是哦那个的简单归纳法。

题 g 在不考虑 $y$ 包含空元素的情况下，读者容易产生疑惑：要如何证明 S 集合中最小的元素 $x_0$ 对 $P$有 $P(x_0)$ 为真？然而根据注解可知，题目中的 y 包含空元素，所以对于 S 中的最小元素 $x_0$ 我们能够从空条件证明出 $P(x_0)$ 为真。

1.2.2 数，幂和对数

容易忽略的幂的定义

对于有理数 $r= p/q$， 定义 $b^r$为：$b^{p / q}=\sqrt[q]{b^{p}}$

实数是有一个十进展开的量 x： $x=n+ 0. d d_2d_3 ···$，十进展开不以无穷多个 9 结尾。

$$n+\frac{d_{1}}{10}+\frac{d_{2}}{100}+\cdots+\frac{d_{k}}{10^{k}} \leqslant x<n+\frac{d_{1}}{10}+\frac{d_{2}}{100}+\cdots+\frac{d_{k}}{10^{k}}+\frac{1}{10^{k}}$$

如 0.23999...不是十进展开，因为 0.24 对于给定的 x，同样满足式。

对于所有实数值 x, 我们定义 $b^x$。我们要求：

$$b^{n+d_{1} / 10+\cdots+d_{k} / 10^{k}} \leqslant b^{x}<b^{n+d_{1} / 10+\cdots+d_{k} / 10^{k}+1 / 10^{k}}$$

因此对于 $b^x$ 我们可以得到任何想要的精度。

当 $b<1$ 时，我们定义 $b^{x}=(1 / b)^{-x}$，当 $b =1$ 时，$b^{x}=1$。

习题参考

• 习题 2. 幂的定义

1+ 0.23999...不是十进展开，根据上述幂的定义，0.24000 对于给定的 x，同样满足定义的表达式，而且不以无穷多个 9 结尾。

• 习题 5

类似十进制展开式，把式子中 10 改成 2，然后不能以无穷多个 1 结尾。

• 习题 22 [20] 证明$lgx \approx ln x + \log_{10} x$

想知道误差多少除一下就知道了

$$\frac {lnx + \log_{10}x}{lgx} = \frac {\frac {lgx}{lge}}{lgx} + \frac {\frac {lgx}{lg_{10}}} {lgx} \\ = \frac 1{lge} + \frac 1{lg_{10}} \approx 0.582\%$$

• 习题 23. [M25] $ln xy = lnx + lny$ 的几何意义

image-20210115205346888

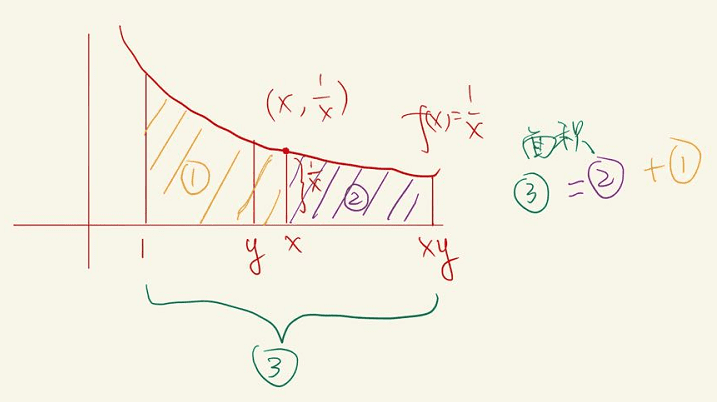
首先给定一个面积为 lny 的图形，那么根据书上的图，这个图形的底应该从 1 到 y。 他的两条高分别为 1 和 1/y。

然后把长拉长 x 倍，高缩小 x 倍。则高变成 1/X 和 1/XY。自然的底就移动到了 X 到 XY。

于是 绿色面积 lnxy = 黄色面积 lnx + 紫色面积 lny

• 习题 25 [22] 计算机计算 $y = log_bx$ 的方法

由 L4 得，

$$X_i = z_i * 2^{\sum k_i} \tag 1$$

由 L3 得，

$$\frac {x_i} {x_i - z_i} = \frac {x_i}{x_{i+1}} = \frac {2^{\sum k_i}}{2^{\sum k_i}-1} \tag2$$

$$\sum_{i=0}^k \frac {x_i}{x_{i+1}} = x_0 \tag3$$

所以，由 等式 2，3 得， $\sum log_b(\frac {2^{\sum k_i}}{2^{\sum k_i}-1}) = log_bx_0$ , 这里 $x_0$ 就是第一个输入的 $x$。

由 L3 得， $x_i \ge 1$, 由等式 2 得，$x_{i+1} < x_i$ 。所以 $x_i$ 会停在 1。

• 习题 26. [M27] 求题 25 得误差上届