Transformer 位置编码小述

绝对位置编码

Transformer 的 Multi-Head-Attention 无法判断各个编码的位置信息。因此 Attention is all you need 中加入三角函数位置编码（sinusoidal position embedding），表达形式为：

$$\begin{array}{l} P E_{(\text {pos }, 2 i)}=\sin \left(\operatorname{pos} / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)}=\cos \left(\operatorname{pos} / 10000^{2 i / d_{\text {model }}}\right) \end{array}$$

其中 pos 是单词位置，i = (0,1,... d_model) 所以d_model为 512 情况下，第一个单词的位置编码可以表示为：

$$P E(1)=\left[\sin \left(1 / 10000^{0 / 512}\right), \cos \left(1 / 10000^{0 / 512}\right), \sin \left(1 / 10000^{2 / 512}\right), \cos \left(1 / 10000^{2 / 512}\right), \ldots\right]$$

BERT、GPT 等也是用了绝对位置编码，但是他们采用的是可学习的绝对位置编码。

相对位置编码

经典相对位置编码

Self-Attention with Relative Position Representations 论文提出了在 self-attention 中加入可学习的相对位置编码，位置 $i,j$ 之间的相对位置信息表示为 $a^K_{ij},a^V_{ij}\in R^{d_z}$ 。注意力计算方式为：

$$e_{i j}=\frac{x_{i} W^{Q}\left(x_{j} W^{K}+a_{i j}^{K}\right)^{T}}{\sqrt{d_{z}}}\\ \alpha_{i j}=\frac{\exp e_{i j}}{\sum_{k=1}^{n} \exp e_{i k}}\\ z_{i}=\sum_{j=1}^{n} \alpha_{i j}\left(x_{j} W^{V}+a_{i j}^{V}\right)$$

论文认为相对位置信息太长并没有用，因此便对位置距离进行了截断：

$$\begin{aligned} a_{i j}^{K} &=w_{\operatorname{clip}(j-i, k)}^{K} \\ a_{i j}^{V} &=w_{\operatorname{clip}(j-i, k)}^{V} \\ \operatorname{clip}(x, k) &=\max (-k, \min (k, x)) \end{aligned}$$

其中 $\left(w_{-k}^{K}, \ldots, w_{k}^{K}\right)=w^{K}\in R^{k\times d_z}$ ，$w^V$ 格式同 $w^K$，都是可学习的参数。但后续实验表明，当 $k\ge 2$ 时，模型的表现效果差别不大。

华为的 NEZHA 采用的也是以上的相对位置编码方式，不同的是 NEZHA 中的 $a^K_{ij},a^V_{ij}$ 均使用 sinusoid encoding matrix：

$$\begin{array}{c} a_{i j}[2 k]=\sin \left((j-i) /\left(10000^{\frac{2 \cdot k}{d_{z}}}\right)\right) \\ a_{i j}[2 k+1]=\cos \left((j-i) /\left(10000^{\frac{2 \cdot k}{d z}}\right)\right) \end{array}$$

NEZHA 表示这样做是为了能够在预测阶段处理更长的序列。

Transformer-XL

Transformer-XL 主要思想是将 RNN 与 Transformer 结合。给定一个文章中连续的两个长度为 $L$ 的片段$s_\tau = [x_{\tau,1}, · · · , x_{\tau,L}]$ 和 $s_{\tau+1} = [x_{\tau+1,1}, · · · , x_{\tau+1,L}]$ ，对于 $s_{\tau+1}$ 的隐状态 $h_{\tau+1}$ ，在计算注意力之前与 $s_{\tau}$ 去除梯度后的隐状态 $h_\tau$ 拼接（仅计算 KV 时拼接，因此 $\widetilde{\mathbf{h}}_{\tau+1}^{n-1}\in R^{2L\times d_z}$ ，$k,v\in R^{2L\times d_h}$ ，$q\in R^{L\times d_h}$）：

$$\begin{array}{l} \widetilde{\mathbf{h}}_{\tau+1}^{n-1}=\left[\mathrm{SG}\left(\mathbf{h}_{\tau}^{n-1}\right) \circ \mathbf{h}_{\tau+1}^{n-1}\right], \\ \mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}=\mathbf{h}_{\tau+1}^{n-1} \mathbf{W}_{q}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{k}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{v}^{\top}, \\ \mathbf{h}_{\tau+1}^{n}=\text { Transformer-Layer }\left(\mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}\right) . \end{array}$$

同时论文针对注意力权重进行了修改。Transformer 采用绝对位置编码下的注意力权重表示为：

$$\begin{aligned} \mathbf{A}_{i, j}^{\mathrm{abs}} &=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(b)} \\ &+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(d)} . \end{aligned}\tag1$$

Transformer-XL 提出了新的相对位置编码方式：

$$\begin{aligned} \mathbf{A}_{i, j}^{\mathrm{rel}} &=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(b)} \\ &+\underbrace{u^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{v^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(d)} \cdot \end{aligned}$$

如果从这个角度来看的话，上节中的经典相对位置编码仅采用了 $(a),(b)$ 两项。相比于使用可学习参数来表示位置之间的关系，Transformer-XL 中 $ij$ 之间的位置关系矩阵 $R_{i-j}$ 为 sinusoid encoding matrix（与 NEZHA 相同）；$u,v\in R^d$ 为可学习参数；用 $W_{k,E},W_{k,R}$ 分别对单词编码和位置编码进行映射。因此一个 Transformer-XL 模块可以表示为：

$$\begin{aligned} \widetilde{\mathbf{h}}_{\tau}^{n-1}=& {\left[\mathrm{SG}\left(\mathbf{m}_{\tau}^{n-1}\right) \circ \mathbf{h}_{\tau}^{n-1}\right] } \\ \mathbf{q}_{\tau}^{n}, \mathbf{k}_{\tau}^{n}, \mathbf{v}_{\tau}^{n}=& \mathbf{h}_{\tau}^{n-1} \mathbf{W}_{q}^{n \top}, \widetilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{k, E}^{n}, \widetilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{v}^{n \top} \\ \mathbf{A}_{\tau, i, j}^{n}=& \mathbf{q}_{\tau, i}^{n}{ }^{\top} \mathbf{k}_{\tau, j}^{n}+\mathbf{q}_{\tau, i}^{n}{ }^{\top} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j} \\ &+u^{\top} \mathbf{k}_{\tau, j}+v^{\top} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j} \\ \mathbf{a}_{\tau}^{n}=& \text { Masked-Softmax }\left(\mathbf{A}_{\tau}^{n}\right) \mathbf{v}_{\tau}^{n} \\ \mathbf{o}_{\tau}^{n}=& \text { LayerNorm }\left(\operatorname{Linear}\left(\mathbf{a}_{\tau}^{n}\right)+\mathbf{h}_{\tau}^{n-1}\right) \\ \mathbf{h}_{\tau}^{n}=& \text { Positionwise-Feed-Forward }\left(\mathbf{o}_{\tau}^{n}\right) \end{aligned}$$

上述 Transformer-XL 的相对位置编码以及 recurrence mechanism 也被应用在了 XLNet 中，同时 XLNet 的 Segment encodings 也采用了相对位置编码的思想，如果位置 $i,j$ 在同一个片段内，则 $s_{ij}=s_+$，反之为 $s_{ij}=s_-$。其中 $s_+,s_-$ 为可学习参数。在计算注意力权重时，将位置之间的相对段落编码加入：$a_{i j}=\left(\mathbf{q}_{i}+\mathbf{b}\right)^{\top} \mathbf{s}_{i j} + a_{origin}$ ，其中 $q_i$ 为 query 编码， $a_{origin}$ 为加入段落相对位置编码前的原始注意力权重。

TENER

TENER 文中分析了 sinusoidal position embedding 的问题，这种位置编码的方式使得任意两个位置的编码 能够传递位置间的距离信息 。对于位置 $t,t+k$ 的编码 $PE_t,PE_{t+k}$ ，他们之间的点积受距离 $k$ 影响：

$$\begin{aligned} P E_{t}^{T} P E_{t+k}=& \sum_{j=0}^{\frac{d}{2}-1}\left[\sin \left(c_{j} t\right) \sin \left(c_{j}(t+k)\right)+\cos \left(c_{j} t\right) \cos \left(c_{j}(t+k)\right)\right] \\ =& \sum_{j=0}^{\frac{d}{2}-1} \cos \left(c_{j}(t-(t+k))\right) \\ =& \sum_{j=0}^{\frac{d}{2}-1} \cos \left(c_{j} k\right) \end{aligned}$$

但对于 Multi-Head-Attention，位置编码并非直接点积，而是先经过了一次线性变换：$P E_{t}^{T} W^T_qW_kP E_{t+k}$。因此距离信息可能在参数学习过程中淡化或者增强。下图表示了 $P E_{t}^{T} P E_{t+k}$（蓝点）及 $P E_{t}^{T} WP E_{t+k}$ （绿、红点）。可以看出对于随机初始化的 $W$，相对位置信息 $k$ 并没有明显的特点。这或许能解释为啥作者在设计位置编码的过程（下文 $(2)$ 式）中没有使用 $W_k$。

相关图片

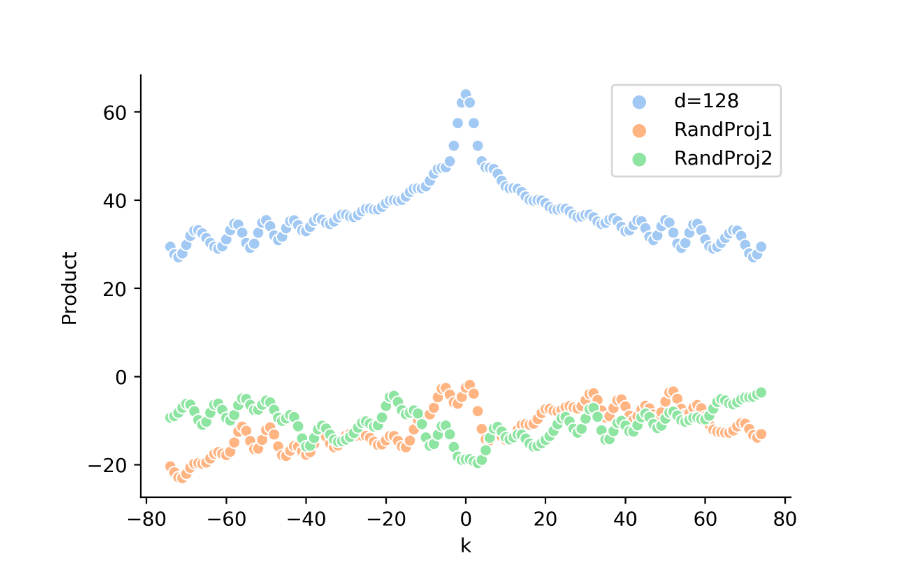
然而正弦位置编码间的点积 无法传递位置方向关系 ：

$$P E_{t}^{T} P E_{t+k}= \sum_{j=0}^{\frac{d}{2}-1} \cos \left(c_{j} k\right)=\sum_{j=0}^{\frac{d}{2}-1} \cos \left(-c_{j} k\right)= P E_{t-k}^{T} P E_{t}$$

该问题使得 vanilla Transformer 在实体识别任务上表现不如 LSTM 系列模型。单词先后顺序对判断实体类别有重要意义，如在例句 福建省位于东南沿海 中，可以根据位于判断其前后名词类别。TENER 提出了新的相对位置编码方式：

$$\begin{array}{l} Q, K, V=H W_{q}, H_{d_{k}}, H W_{v} \\ R_{t-j}=\left[\ldots \sin \left(\frac{t-j}{10000^{2 i / d_{k}}}\right) \cos \left(\frac{t-j}{10000^{2 i / d_{k}}}\right) \ldots\right]^{T} \\ A_{t, j}^{r e l}=Q_{t} K_{j}^{T}+Q_{t} R_{t-j}^{T}+\mathbf{u} K_{j}^{T}+\mathbf{v} R_{t-j}^{T} \\ \operatorname{Attn}(Q, K, V)=\operatorname{softmax}\left(A^{r e l}\right) V \end{array}\tag2$$

该方案与 Transformer-XL 相似，引入了两个可学习参数 $u,v\in R^d$，以及相对位置信息 $R_{t-j}$，比较特别的是 $K=H_{d_{k}}$ ，去掉 $W_k$ 是为了减小模型复杂度，增强模型在小规模 NER 数据集上的学习效果。

此外 TENER 还采用了 Un-scaled Dot-Product Attention 没有对 $A^{rel}_{t,j}$ 除以 $\sqrt d_k$。论文猜测这样实验效果更好是由于 NER 任务中的样本不均衡导致的。但个人猜测以保持注意力运算中二阶矩不变的角度出发，将 $A^{rel}_{t,j}$ 除以 $2\sqrt d_k$ 效果可能会更好。

T5

T5 中采用了更简单的位置编码方式：$A=E_iE_j + \beta_{ij}$。论文称 $\beta_{ij}$ 为可学习参数，所有层之间共享，Attention 中不同头使用的位置编码不一样。但在根据部分博主对源码的描述，T5 使用了固定的 $\beta_{ij}$ ，并且根据 $i-j$ 对 $\beta_{ij}$ 进行了分桶处理。如：$\beta_{ij}=(i-j),if\ i-j<8$，$\beta_{ij} = 8, if\ 8\le i-j<14$ 等。该做法符合直觉：相对距离的边际效应随距离增大而逐渐减小。

DeBERTa

DeBERTa 提出了解耦注意力（DISENTANGLED ATTENTION ），考虑公式 $(1)$ 中的分解注意力权重方案，其可分为四项：内容-内容,内容-位置,位置-内容,位置-位置 。经典款中保留了前两者，Transformer-XL 、TENER 保留了全部，T5 保留了内容-内容与位置-位置。在 DeBERTa 保留了前三者：

$$\begin{aligned} \boldsymbol{Q}_{c}=\boldsymbol{H} \boldsymbol{W}_{\boldsymbol{q}, c}, \boldsymbol{K}_{c}=&\boldsymbol{H} \boldsymbol{W}_{\boldsymbol{k}, c}, \boldsymbol{V}_{c}=\boldsymbol{H} \boldsymbol{W}_{\boldsymbol{v}, \boldsymbol{c}}, \boldsymbol{Q}_{\boldsymbol{r}}=\boldsymbol{P} \boldsymbol{W}_{\boldsymbol{q}, \boldsymbol{r}}, \boldsymbol{K}_{\boldsymbol{r}}=\boldsymbol{P} \boldsymbol{W}_{\boldsymbol{k}, \boldsymbol{r}} \\ \tilde{A}_{i, j}=& \underbrace{Q_{i}^{c} K_{j}^{c \top}}_{\text {(a) content-to-content }}+\underbrace{\boldsymbol{Q}_{i}^{c} \boldsymbol{K}_{\boldsymbol{\delta}(i, j)}^{r \top}}_{\text {(b) content-to-position }}+\underbrace{\boldsymbol{K}_{j}^{c} \boldsymbol{Q}_{\delta(j, i)}^{r \top}}_{\text {(c) position-to-content }} \\ \boldsymbol{H}_{\boldsymbol{o}}=& \operatorname{softmax}\left(\frac{\tilde{\boldsymbol{A}}}{\sqrt{3 d}}\right) \boldsymbol{V}_{c} \end{aligned}\tag 3$$

$Q,K,V\in R^{L\times d}$，$W\in R^{d\times d}$，$P\in R^{2k\times d}$，$k$ 为超参：位置距离上限。

其中相对位置信息也采取了截断：

$$\delta(i, j)=\left\{\begin{array}{rcl} 0 & \text { for } & i-j \leqslant-k \\ 2 k-1 & \text { for } & i-j \geqslant k \\ i-j+k & \text { others. } & \end{array}\right.$$

此处对 $\boldsymbol{A}$ 除以 $\sqrt {3d}$，个人猜测是由于作者假设 $(3)$ 式中 $(a),(b),(c)$ 相互独立，若 $Q,K$ 方差为 1，期望为 0，那么：

$$\begin{aligned} \mathbb{E}\left[(\boldsymbol{q} \cdot \boldsymbol{k})^{2}\right] &=\mathbb{E}\left[\left(\sum_{i} q_{i} k_{i}\right)\left(\sum_{j} q_{j} k_{j}\right)\right]=\sum_{i} \mathbb{E}\left[q_{i}^{2}\right] \mathbb{E}\left[k_{i}^{2}\right]=d \end{aligned}$$

因此 $(a),(b),(c)$ 各自方差为 $d$，要保持输出方差为 1 的话，则需要对 $A$ 除以 $\sqrt {d\times 3}$，hugging face 上的 DeBERTa 代码 scale_factor = 1 + len(self.pos_att_type) 也与该猜想符合，其中 self.pos_att_type=['p2c','c2p] 。（源码别看论文上的 MircoSoft 仓库链接，那边写的 DeBERTa 细节有亿点点不一样。​​）

此外，DeBERTa 还在模型中加入了绝对位置编码信息，前 m 层 Transformer 模块论文作者总成为 Encoder，只使用相对位置信息。后 n 层 Transformer 模块，论文作者成为 EMD（Enhanced Masked Decoder），加入了绝对位置信息。（但笔者在 hugging face 源码中并未找到相关配置，头疼）。

参考

[1] NEZHA: NEURAL CONTEXTUALIZED REPRESENTATION FOR CHINESE LANGUAGE UNDERSTANDING [2] Self-Attention with Relative Position Representations [3] Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context [4] TENER: Adapting Transformer Encoder for Named Entity Recognition [5] Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer [6] DEBERTA: DECODING-ENHANCED BERT WITH DISENTANGLED ATTENTION [7] 让研究人员绞尽脑汁的 Transformer 位置编码 [8] 层次分解位置编码，让 BERT 可以处理超长文本