Aho-Corasick 多字符串匹配加速算法。文章包括 Tire, KMP, Aho-Corasick

需要匹配的单词有 n 个，要在一篇具有 m 个单词的文章中找出他们的位置。

AC 自动机可以理解为 Tire 与 KMP 算法的结合。使用 fail 指针加速了字符串匹配的速度。

Trie

前缀树/字典树 的插入、查询时间复杂度均为 为 $O(|S|)$，其中 $|S|$ 是每次插入或查询的字符串的长度。空间复杂度为 $O(|T|·\sum)$ 其中 $|T|$ 为插入字符串长度之和，$\sum$ 为字符集大小。

Divide-and-conquer is easy to understand, but hard to create. This article will discuss the key for proofing Divide-and-conquer as well as some ideas for solving a new problem using divide-and-conquer based on these 4 topics: Merge Sort, Quick Sort, Hanoi and Closet Point

开篇：关于这本书和算法

（我）阅读次书主要为了理解计算机程序实现算法整个过程，一个只能表示 0 和 1 的机器，是如何高效的进行一系列运算，最后得到我们所提问题的结果。算法优化不仅应该停留在数学层面上的优化，也应该针对算法实现的过程进行优化。而今科技日新月异，传统计算机被摩尔定律等条件限制了发展的速度，希望能从本书中获得一些启发来把握新科技技术的优势（如量子计算机）使算法能够以最高效的方式运行。

这系列博客将用来记录我阅读中遇到的重点信息，个人笔记，或者有趣的题目:) 。你可以通过标签 TAOCP 或 计算机程序艺术 找到他们。对于本书中那些参考答案奇怪的题目，我会尽力给出详细合理的答案。

本文参考《计算机程序艺术》第 3 版 国防工业出版社 及《Knuth D. - The art of computer programming. Volume 1-AW (1968) 》，对于中文版书籍与英文原著表达不一处，均已原著为准。

公式很多，预期加载时间 1 分钟。

Dijkstra

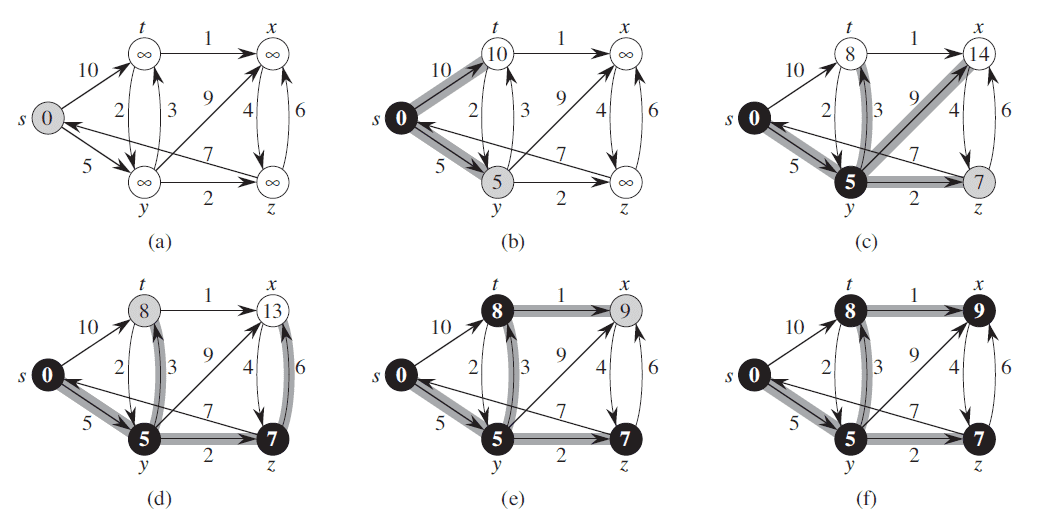
(图片来源 : CLRS p659 24.3)

原版算法

先来看看代码

import math, heapq

for u in vertex:  # 这边对所有点都进行了一次 Dijkstra
    heap = []
    for v in vertex:
        if v != u:
            heapq.heappush(heap, [adj[u][v] if v in adj[u] else math.inf, v])  #提取到达距离最小的节点
    dist = {u: 0}
    while len(heap) > 0:
        mindist, v = heapq.heappop(heap)
        dist[v] = mindist
        for i in range(len(heap)):
            if heap[i][1] in adj[v]:
                heap[i][0] = min(heap[i][0], mindist + adj[v][heap[i][1]])
        heapq.heapify(heap)